Тригнометрийн тэнцэл бишийг бодохдоо алгебрын тэнцэл бишийн шинжүүд болон төрөл бүрийн тригнометрийн хувиргалт, томьёонуудыг ашиглана. Тригнометрийн тэнцэл бишийг бодоход нэгж тойрогийг ашиглах нь бараг гарцаагүй байдаг.
Жишээ 1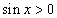 тэнцэл бишийг бод.
тэнцэл бишийг бод.
Бодолт
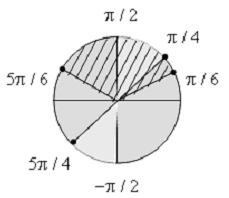
Нэгж тойргийн радиусын нэг эргэлтэд энэ тэнцэл биш нь 0 < x < π үнэн байна. Одоо синусын үе 2πn ийг нэмэх шаардлагатай. : 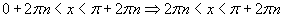
Жишээ 2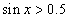 тэнцэл бишийг бод.
тэнцэл бишийг бод.
Бодолт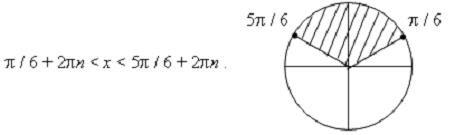
Жишээ 3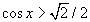 тэнцэл бишийг бод.
тэнцэл бишийг бод.
Бодолт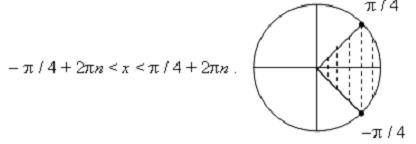
Жишээ 4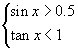 тэнцэл бишийг бод.
тэнцэл бишийг бод.
Бодолт
Эхний тэнцэл биш 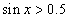
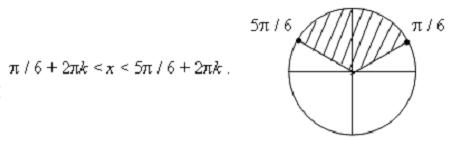
шийдтэй. Хоёрдугаар тэнцэл биш 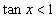
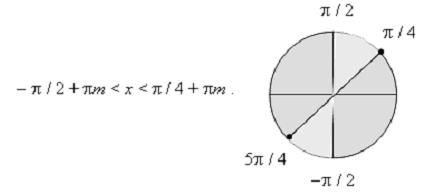
шийдтэй. Энэ хоёр шийдийг нэгтгэвэл ерөнхий шийд гарна.
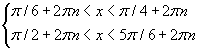
Шийдийн муж нь хоёр шийдийн давхцал байна.





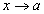 үед a цэгийн орчимд дифференциалчлагддаг f(x), g(x) функцуудын хувьд
үед a цэгийн орчимд дифференциалчлагддаг f(x), g(x) функцуудын хувьд 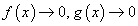 эсвэл,
эсвэл, 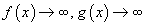 эсвэл
эсвэл 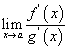 хязгаар байна.
хязгаар байна.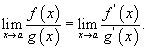 байна.
байна.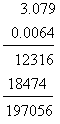
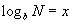 Энэ бичлэг нь
Энэ бичлэг нь 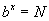 гэсэнтэй адил.
гэсэнтэй адил.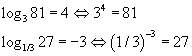
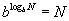 адитгал байдлаар бичиж болно.
адитгал байдлаар бичиж болно. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.