Үл мэдэгдэгч нь тригнометрийн функцэд байгаа тэгшитгэлийг тригнометрийн тэгшитгэл гэнэ.
Тригнометрийн энгийн тэгшитгэлүүд
| 1 | sin x=0, x=πk, k | 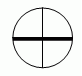 |
| 2 | sin x=1, x=π/2 + 2πk, k | 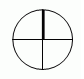 |
| 3 | sin x=-1, x=-π/2 + 2πk, k | 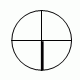 |
| 4 | sin x=a , |a| > 1 | |
| 5 | sin x=a, |a|≤1 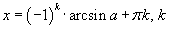 |
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах




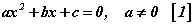 хэлбэрийн тэгшитгэлийг
хэлбэрийн тэгшитгэлийг 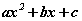 илэрхийллийг
илэрхийллийг 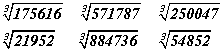
 тэгшитгэлийг бод.
тэгшитгэлийг бод.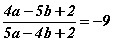 бол
бол 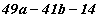 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.