Натурал n тооноос хамаарсан тодорхой шинжийг батлах хэрэгтэй боллоо гэж бодъё. Энэ шинж нь томьёо, адитгал, тэнцэл биш, нотолгоо байж болно. Хэрвээ
Энэ шинж ямар нэгэн n0 натурал тооны хувьд үнэн
n=k үед энэ шинж үнэн байх нөхцлөөс үүдэн дурын k≥ n0 хувьд n=k+1 үед энэ шиж үнэн гэвэл энэ шинж нь дурын n≥ n0 натурал тооны хувьд үнэн байна.
Жишээ:
1+3+5+ … +(2n-1)=n² гэдгийг батал.
Бодолт:
Тэнцлийн баталгаанд математик индукцийн аргыг хэрэглэе. n=1 үед тэнцэл үнэн гэдэг нь ойлгомжтой байна. 1=1²
Тэгвэл ямар нэгэн k тооны хувьд тэнцлийг үнэн гэе. Өөрөөр хэлбэл
1+3+5+ … +(2k-1)=k²
тэнцэл үнэн гэсэн үг. Тэгвэл k+1 үед тэнцэл үнэн гэдгийг баталъя. Өгөгдсөн тэнцлийг n=k+1 тохиолдолд авч үзье.
1+3+5+ … +(2k-1)+(2k+1)=k²+(2k+1)=(k+1)²
Эндээс математик индукцийн нөхцлөөр k тооны хувьд тэнцэл биелэгдэнэ гэдгээс k+1 тохиолдолд тэнцэл үнэн боллоо. Тэгвэл дурын n натурал тооны хувьд тэнцэл хүчинтэй болсноор баталагдлаа.
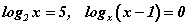
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.