Шулуун дээр орших дурын цэгээс нэг зүгт байрлах шулууны хэсгийг цацраг гэнэ. Эндээс цацрагийг хагас шулуун ч гэж бас нэрлэдэг. Цацраг эхлэл болон чиглэлтэй байдаг. Цацраг эхлэж буй цэгийг цацрагийн эхлэл, эхлэлийн цэг эсхүл цацрагийн орой гэж хэлнэ. Эндээс цацрагт эхлэл байхаас төгсгөл гэж байдаггүй.
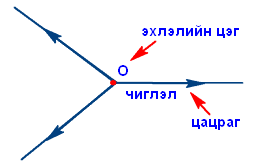
Зурагт үзүүлсэн гурван цацраг ерөнхий эхлэлтэй ч өөр чиглэлтэй. Аль ч цацрагийг O цэгээс гарсан цацраг гэж нэрлэж болно.
Нэмэлт цацраг.
Шулуун дээрх дурын цэг тухайн шулууныг хоёр хагас шулуунд хуваана. Өөрөөр хэлбэл хоёр хэсэг буюу цацрагт гэсэн үг. Эдгээр хэсэг бүрийг нөгөө цацрагийн хувьд нэмэлт цацраг гэж нэрлэдэг.
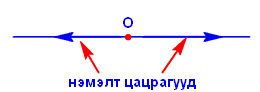
Эндээс нэг шулуун дээр орших, ерөнхий эхлэлтэй, эсрэг чиглэлтэй цацрагуудыг нэмэлт цацрагууд гэсэн тодорхойлолт гарч ирнэ.
Цацрагуудын тэмдэглэгээ.
Цацрагийг нэг жижиг латин үсгээр тэмдэглэнэ.
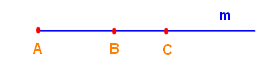
Жишээ нь зурагт үзүүлсэн цацрагтйг m цацраг гэж тэмдэгдэж болохын дээр цацраг дээрх цэгүүдээр бас тэмдэглэж болно. Жишээ нь AB эсхүл AC гэж. Цацраг дээрх хоёр цэгээр түүнийг тэмдэглэхдээ эхний цэг нь цацрагийн эхлэлийг заана. Зураг үзүүлсэн цацрагийг BC гэж тэмдэглэвэл B цэгээс эхлэх цацраг болох тул болохгүй. Эндээс ямар нэгэн бодлого, асуулт, материалд AB цацраг гэсэн байвал түүнийг A цэгээс эхлэлтэй цацраг дээр B цэг оршино гэж ойлгох хэрэгтэй.
Санамж: Аливаа зүйлийн анхдагч ухагдхуунууд энгийн болоод ойлгомжтой байдгаас сурагчид хөнгөн юм гэж үзэн анхаарахгүй орхисноос хоцрогдол үүсэн сүүлдээ тухайн хичээлээс зугтаах үндсэн шалтгаан болдог. Хичээлд тайлбарлаж буй ухагдхууныг сайтар ойлгон тогтоон авахуулахын тулд хичээлүүдийг аль болохоор богинохон байлгахыг хичээх болно. Геометрийн суурь ухагдхуунуудыг мэдэхгүйгээр цааш явахгүй гэдгийг сануулъя. Та цагаан толгойн үсгүүдийг бүгдийг тогтоогоогүй бол уншиж чадахгүйн адил ямарч хичээлийн үндсэн ойлголтыг мэдэхгүйгээр түүнийг сурна гэж байхгүй.





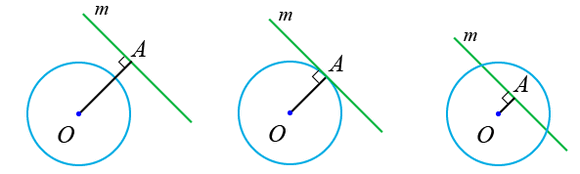
 функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.