ax+b=0 хэлбэрийн тэгшитгэтгэлийг нэг үл мэдэгдэгчтэй шугаман тэгшитгэл гэнэ. Энд a , b нь тодорхой тоонууд харин x нь үл мэдэгдэгч болно.
Тэгшитгэлийг бодно гэдэг нь тэгшитгэлийг адитгал болгох x үл мэдэгдэгчийн тоон утгыг олно.
- Хэрэв a≠0 бол тэгшитгэлийн шийд нь
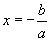
- Хэрэв a=0 бол хоёр тохиолдол гарна.
- b=0 бол 0·x+0=0 энд x дурын тоо байж болно.
- b≠0 бол 0·x+b=0 энд тэгшитгэл шийдгүй.
Жишээ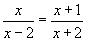 
тэгшитгэлийг бод. Диагналын дагуу илэрхийллүүдийг хооронд нь үржүүлбэл 
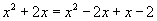гарна. Тэгшитгэлийн бүх гишүүдийг тэнцүүгийн тэмдгийн зүүн талд гаргавал 3x+2=0 гэсэн тэгшитгэл гарна. Эндээс x=-2/3.
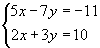тэгшитгэлийн системийг бод.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.