Дурын геометрийн гүдгэр дүрсний периметр нь түүний бүх талуудын нийлбэртэй тэнцүү байдаг тул тэгш өнцөгт, квадрат, ромб зэрэг дөрвөн өнцөгтийн периметрийг түүний дөрвөн талын нийлбэрээр тодорхойлж болно.
Жишээ болгоод доорх зурагт үзүүлсэн гурван дөрвөн өнцөгтийн периметрийг
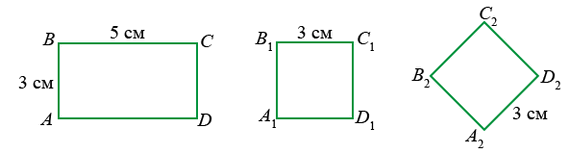
тооцохыг харцгаая. Тэгш өнцөгт 3 см урттай хоёр талтай, 5 см урттай хоёр талтай учраас түүний периметрийг дээрх тодорхойлолтоор P = AB + BC + CD + DA = 3 см + 5 см + 3 см + 5 см = 16 см гэж олж болно.
Квадрат, ромб нь дөрвөн ижил талтай байдаг тул тэдгээрийн периметр
Квадратын хувьд P = A1B1 + B1C1 + C1D1 + D1A1 = 3 см + 3 см + 3 см + 3 см = 12см
Ромбын хувьд P = A2B2 + B2C2 + C2D2 + D2A2 = 3 см + 3 см + 3 см + 3 см = 12 см байна.
Дээрх дөрвөн өнцөгтүүдэд ижил урттай талууд байгаа учраас периметрийг талуудын нийлбэрээс гадна ижил талуудын үржвэрээр орлуулан тооцох боломжтой. Жишээ нь тэгш өнцөгтийн хувьд
P = 3 см + 5 см + 3 см + 5 см = 3 см · 2 + 5 см · 2 = (3 см + 5 см)2 = 8 см · 2 = 16 см гэж тооцох боломжтой.
Эндээс тэгш өнцөгтийн периметр түүний хамар орших талуудын /суурь, өндөр/ уртыг хоёроор үржүүлэн нэмсэн нийлбэртэй тэнцүү гэсэн дүгнэлтийг хийж болох бөгөөд тэгш өнцөгтийн периметрийг олох P = (a + b)2 ерөнхий томьёо гарч ирнэ. Энд P - тэгш өнцөгтийн периметр харин a, b - түүний хамар талууд.
Квадрат, ромб нь дөрвөн ижил талтай тул периметрийг үржвэрээр P = 3 см + 3 см + 3 см + 3 см = 3 см · 4 = 12 см гэж олж болно. Эндээс квадрат, ромбын периметр нь түүний талыг 4 -өөр үржүүлсэн тэнцүү буюу P = a · 4 гэсэн ерөнхий томьёо гарч ирнэ. Энд P - квадрат, ромбын периметр харин a - аль нэг дөрвөн талын нэгийнх урт.
Санамж: Зарим сурагчдад хичээл энгийн бүр хэрэггүй мэт санагдаж болно. Периметр ойлголтыг сайн ойлгосон сурагчид энэ хичээл нэг их юм өгөхгүй нь ойлгомжтой. Гэхдээ ЕБС -ийн геометрийн хичээлийн хавтгайн геометр сэдвийн бүхий л ойлголт ухагдхууныг багтаасан Хавтгайн геометр хичээлийн багц танд хэрэгтэй зүйлийг өгнө гэдэгт итгэж болно. Онолын мэдлэг нимгэн бол бодлогын шийдлийг олоход илүү хүнд. Энэ нь ялангуяа геометрийн бодлогод илүү мэдрэгддэг гэдэг нь сурагчид геометрийн бодлогод нилээд муу байдгаар батлагддаг.





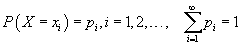
 задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.