Хичээлд хавтгайн геометрийн бодлого бодоход чухал хэрэгтэй гурвалжны биссектрисийн нэгэн чанарыг авч үзье. ABC гурвалжны B оройгоос түүний эсрэг орших AC тал дээрх D цэгт биссектрисийг буулгая.
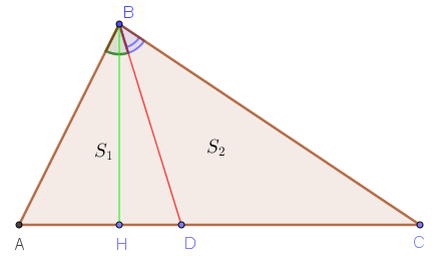
BD хэрчим нь ABC гурвалжны B оройгоос буулгасан биссектрис.
Гурвалжны биссектрис эсрэг орших талыг харгалзах хажуу талуудын харьцаатай тэнцүү харьцаатай хэрчмүүдэд хуваадаг. Өөрөөр хэлбэл 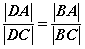 гэсэн үг.
гэсэн үг.
Баталгаа.
Гурвалжны оройн өнцгийг хуваасан хэрчмийг биссектрис гэдгийг Гурвалжин хичээлээс мэднэ. Тэгэхлээр 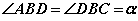 байна гэсэн үг. Цааш биссектрисээр хуваагдсан ABD, BDC гурвалжингуудын талбайн харьцааг олцгооё. Үүнийг гурвалжны хоёр тал тэдгээрийн хоорондох өнцгөөр талбайг олдог
байна гэсэн үг. Цааш биссектрисээр хуваагдсан ABD, BDC гурвалжингуудын талбайн харьцааг олцгооё. Үүнийг гурвалжны хоёр тал тэдгээрийн хоорондох өнцгөөр талбайг олдог 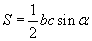 томьёогоор олбол
томьёогоор олбол 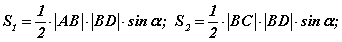 байх бөгөөд харьцааг олбол
байх бөгөөд харьцааг олбол 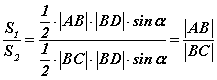 гэж гарна.
гэж гарна.
Нөгөө талаас гурвалжны B оройгоос AC талд BH өндөрийг буулгаад гурвалжны талбайг нэг тал өндрөөр олдог 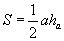 томьёогоор ABD, BDC гурвалжингуудын талбайг олбол
томьёогоор ABD, BDC гурвалжингуудын талбайг олбол 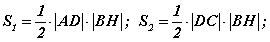 гэж гарах ба талбайг харьцуулбал
гэж гарах ба талбайг харьцуулбал 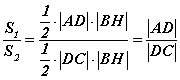 гэж гарна. Хоёр аргаар олсон талбайн харьцаануудаас
гэж гарна. Хоёр аргаар олсон талбайн харьцаануудаас 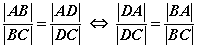 гэж гарснаар чанар батлагдана.
гэж гарснаар чанар батлагдана.
Биссектрисийн урт
ABC гурвалжны A оройгоос татсан биссектрисийн урт гурвалжны A оройн өнцгийг үүсгэх хоёр талын уртын үржвэрээс A оройн эсрэг тал биссектрисээр хуваагдах хоёр хэрчмийн уртын үржвэрийг хасаад язгуур авсантай тэнцүү гэдэг биссектрисийн чухал теорем байдаг.
Баталгаа.
 Теоремийн баталгааг ЕБС-д хийгээд байх нь ховор ч теоремийг илүү сайн ойлгох, геометрийн байгуулалт, бодлого бодох аргачлалыг эзэмшихэд теоремийн баталгаа чухал ач холбогдолтой. Иймээс теоремийн баталгааг хийе.
Теоремийн баталгааг ЕБС-д хийгээд байх нь ховор ч теоремийг илүү сайн ойлгох, геометрийн байгуулалт, бодлого бодох аргачлалыг эзэмшихэд теоремийн баталгаа чухал ач холбогдолтой. Иймээс теоремийн баталгааг хийе.
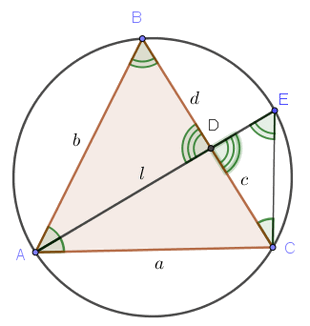
Баталгааны бүрэн зургийг өгсөн тул өөрсдөө зургийг гаргаад яваарай.
Теоремийн үгээр тодорхойлсонг ойлгоход зарим үед хүнд байх тал бий. Иймээс ABC гурвалжин байгуулаад A оройгоос биссектрисийг татахад BC талыг D цэгт огтолсон гэж үзээд түүний уртыг |AD|=l гэе. A оройн өнцгийг үүсгэх хоёр талын уртыг a, b харин BC талыг биссектрис D цэгт огтлон үүсгэх хэрямүүдийн уртыг c, d гэе. Тэгвэл теоремоор 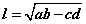 гэдгийг батлая.
гэдгийг батлая.
Теоремийг батлахын тулд ABC гурвалжинг багтаасан тойргийг татаад AD биссектрисийг тойрогтой огтлолцох хүртэл үргэлжлүүлэн огтлолын цэгийг E гээр тэмдэглээд C оройтой холбосон EC хэрчмийг татъя.
AD биссектрис тул 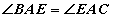 гэдгээс гадна BE нумд BAE ба BCE өнцгүүд тулж байгаа учраас
гэдгээс гадна BE нумд BAE ба BCE өнцгүүд тулж байгаа учраас 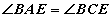 байна. Тэнцүү өнцгүүдийг зурагт ижил тэмдэгүүдээр тэмдэглэе. Үүнээс гадна AC нумд ABC ба AEC өнцгүүд тулж байгаа учраас
байна. Тэнцүү өнцгүүдийг зурагт ижил тэмдэгүүдээр тэмдэглэе. Үүнээс гадна AC нумд ABC ба AEC өнцгүүд тулж байгаа учраас 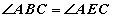 харин D цэгт оройтой
харин D цэгт оройтой 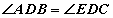 босоо өнцгүүд бас хоорондоо тэнцүү гэдгийг Хамар болон босоо өнцгүүд хичээлээс мэднэ. Ингэснээр хоёр өнцөг тэнцүү шинжээр
босоо өнцгүүд бас хоорондоо тэнцүү гэдгийг Хамар болон босоо өнцгүүд хичээлээс мэднэ. Ингэснээр хоёр өнцөг тэнцүү шинжээр 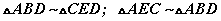 төстэй гурвалжингууд бий болсон.
төстэй гурвалжингууд бий болсон.
Гурвалжин төстэй байх шинжүүд хичээлийг үзээрэй. Эндээс төстэй талуудын порпорционал харьцааг бичвэл 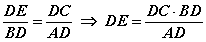 болох бөгөөд утгуудыг тавибал
болох бөгөөд утгуудыг тавибал 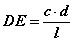 болно. Дараагийн төстэй хос гурвалжингуудаас
болно. Дараагийн төстэй хос гурвалжингуудаас 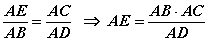 ба утгуудыг тавивал
ба утгуудыг тавивал 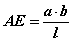 болно. AE=AD+DE тул l=AE-DE гэж бичиж болно. AE, DE утгуудыг тавивал
болно. AE=AD+DE тул l=AE-DE гэж бичиж болно. AE, DE утгуудыг тавивал
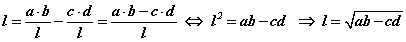 гарснаар теорем батлагдсан.
гарснаар теорем батлагдсан.





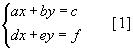 хэлбэрийн тэгшитгэлийн системийг
хэлбэрийн тэгшитгэлийн системийг 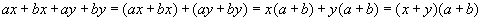
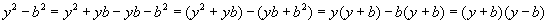
 функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.