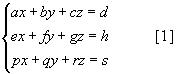 хэлбэрийн тэгшитгэлийн системийг гурван үл мэдэгдэгчтэй гурван шугаман тэгшитгэлийн систем гэнэ. Энд a, b, c, d, e, f, g, h, p, q, r, s өгөгдсөн тоонууд, x, y, z үл мэдэгдэгчид. a, b, c, e, f, g, p, q, r үл мэдэгдэгчдийн коэффициент, d, h, s сул гишүүд юм. Ийм тэгшитгэлийн системийг үндсэн хоёр аргаар /орлуулах, нэмэх ба хасах/ боддог. Энд бид зөвхөн Крамерын аргыг дэлгэрэнгүй авч үзнэ. Эхлээд гуравдугаар эрэмбийн тодорхойлогч гэдэг ойлголтыг авч үзье. Дараах илэрхийллийг
хэлбэрийн тэгшитгэлийн системийг гурван үл мэдэгдэгчтэй гурван шугаман тэгшитгэлийн систем гэнэ. Энд a, b, c, d, e, f, g, h, p, q, r, s өгөгдсөн тоонууд, x, y, z үл мэдэгдэгчид. a, b, c, e, f, g, p, q, r үл мэдэгдэгчдийн коэффициент, d, h, s сул гишүүд юм. Ийм тэгшитгэлийн системийг үндсэн хоёр аргаар /орлуулах, нэмэх ба хасах/ боддог. Энд бид зөвхөн Крамерын аргыг дэлгэрэнгүй авч үзнэ. Эхлээд гуравдугаар эрэмбийн тодорхойлогч гэдэг ойлголтыг авч үзье. Дараах илэрхийллийг
Материалыг бүртгэлтэй хэрэглэгч үзнэ.
how_to_regБүртгүүлэх




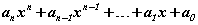 гэсэн ерөнхий хэлбэртэй байдаг. n=1 бол
гэсэн ерөнхий хэлбэртэй байдаг. n=1 бол 
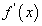 нь x0 цэгт дифференциалчлагдаж байвал түүнийг f(x) функцын x0 цэг дээрх хоёрдугаар эрэмбийн уламжлал /
нь x0 цэгт дифференциалчлагдаж байвал түүнийг f(x) функцын x0 цэг дээрх хоёрдугаар эрэмбийн уламжлал / 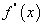 гэж тэмдэглэнэ./ гэнэ.
гэж тэмдэглэнэ./ гэнэ.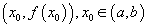 цэгт y=f(x) функцын графикийн муруйд татсан шүргэгчийн доор байрлаж байвал f(x) функцыг (a,b) интервалд гүдгэр гэнэ.
цэгт y=f(x) функцын графикийн муруйд татсан шүргэгчийн доор байрлаж байвал f(x) функцыг (a,b) интервалд гүдгэр гэнэ.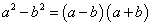 , кубуудын ялгавар
, кубуудын ялгавар 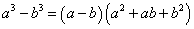 томьёонуудыг ихээр ашигладаг. Тэгвэл дөрөв, тав гэх мэтээр n зэргийн ялгаваруудад тохирох
томьёонуудыг ихээр ашигладаг. Тэгвэл дөрөв, тав гэх мэтээр n зэргийн ялгаваруудад тохирох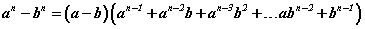
 функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.