Хавтгайн геометрийг зөв ойлгохын суурь бол түүний үндсэн ухагдхуунуудыг маш сайн ойлгосон байх юм. Үндсэн ухагдхууныг ойлгоогүй бол геометрийн бодлого, асуултыг ойлгон зураг гаргах, асуудлыг шийдэх зэргийг давна гэдэг хэцүү. Хичээлээр хавтгай болон геометрийн дүрсүүд ухагдхууныг авч үзье.
Хавтгай.
Хавтгай гэдэг нь орон зайд тэгш, гөлгөр, бүх тал руу хязгааргүй тархсан гадургуу юм.
Зурагт хавтгайн хэсгийг харуулсан болно.
Хязгааргүй тархасан гадаргуу тул түүнд хил байхгүй гэсэн үг. Иймээс хавтгайг ихэндээ тодорхой хэсгээр таслан авч үзэх нь илүү. Учир нь геометрт хавтгайг бүхэлд нь эзэлсэн зүйлийн талаар ярих утгагүй бөгөөд тухайн асуудалд яригдан буй дүрс, биетүүд ямар нэгэн хавтгай буюу түүний тодорхой хэсэгт байрлаж байгаа гэж үздэг.
Хавтгайнууд орон зайд байрлах тул өөр хоорондоо паралел, огтлолцсон, перпендикуляр гэх мэтээр олон төрлөөр байрлаж болно.
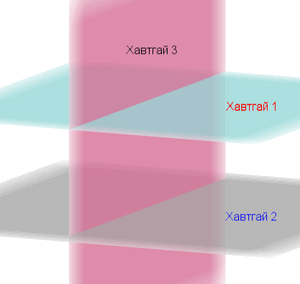
Зурагт гурван хавтгайг үзүүлсэн. Хавтгай1 , Хавтгай2 паралел бол Хавтгай3 нөгөө хоёртойгоо перпендикуляраар огтлолцсон.
Хагас хавтгай.
Хавтгай лээр ямар нэгэн шугам татвал хавтгай шугамаар хоёр хэсэгт хуваагдана. Эндээс хавтгай дээрх шугамаар таслагдсан хэсгийг хагас хавтгай гэнэ.
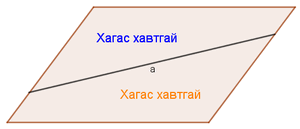
Зурагт хавтгайд a шулуун татан түүнийг хоёр хагас хавтгайд хуваасан. Муруй шугам татсан ч хоёр хагас хавтгайд хуваагдана. Гэхдээ хагас хавтгайнууд анхдагч хавтгайдаа байрлана гэдгийг ойлгох ёстой.
Геометрийн цэг.
Геометрийн цэг бол ямарч хэмжэгдэх шинж болон хэсэггүй абстракт обьект юм. Үүнийг сайн ойлгох ёстой. Өөрөөр хэлбэл цэг нь хавтгай эсхүл орон зай дахь тодорхой байрлалыг заана. Цэгүүдийг A, B, C ... гэх мэтээр латин том үсгээр тэмдэглэдэг. Цэг хэдийгээр абстракт обьект ч гэсэн геометрийн бүх дүрс, биетүүдийн суурь болдог. Энэ нь геометрийн дурын дүрс биетийг тодорхой байдлаар байрласан цэгүүдийн олонлог гэж үзэж болно гэсэн үг.
Геометрийн биетүүд.
Геометрийн биет гэдэг нь цэг, шугам, гадаргуунуудын дурын хослолыг хэлнэ. Геометрийн биетүүд хавтгай болон орон зайн гэсэн хоёр хэсэгт хуваагдана.
Дүрсийг үүсгэх бүх цэгүүд нэг хавтгайд байрлах дүрсийг геометрийн хавтгай биет буюу дүрс гэнэ.
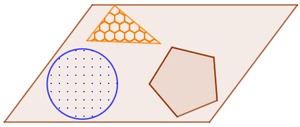
Дээрх зурагт үзүүлсэн дүрсүүдийг бүрдүүлж буй цэгүүд бүгд нэг хавтгай дээр байрлах тул эдгээр нь хавтгай дүрсүүд юм.
Дүрсийг үүсгэх цэгүүд бүгд нэг хавтгайд байрлахгүй дүрсийг геометрийн орон зайн биет гэнэ.
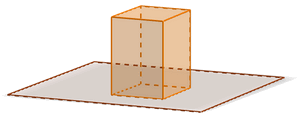
Зурагт үзүүлсэн биетийн доод суурь нэг хавтгайд нөгөө талстууд өөр хавтгайд байрлах учраас биет нь орон зайн биет гэсэн үг.
Нэг хавтгайд байрласанг хавтгай дүрс харин олон хавтгайд байрласанг орон зайн биет гэж ойлгоход болно.
тэгшитгэлийн нэг язгуур нь эерэг, нөгөө язгуур нь сөрөг байх параметрийн бүх утгыг ол.
болох бөгөөд энэ тэнцэтгэл бишийг бодвол 
үед манай тэнцэтгэл бишийн шийдийн нэг нь эерэг нөгөө нь сөрөг байна.
функц [1;9] завсарын аль хэсэгт буурах вэ?
функцийн хамгийн бага утгыг ол.