Тэгшитгэлийн системийг бодох Гауссын арга

Алгебрийн шугаман тэгшитгэлүүдийн системийг (АШТС) бодоход Гауссын арга их тохиромжтой. Энэ арга бусад аргуудтай харьцуулахад хэдэн давуу талтай.

  1. Тэгшитгэлийн системийг зохицож байгаа  эсэхийг урьдчилан шалгах шаардлагагүй
  2. Гауссын аргаар тэгшитгэлийн тоо нь үл мэдэгдэгчийн тоотой тохирсон системийг бодож болохын дээр тэгшитгэлийн тоо нь үл мэдэгдэгчийн тоотой тохирохгүй эсхүл үндсэн матрицийн тодорхойлогч тэгтэй тэнцүү системийг ч бодож болдог
  3. Гауссын арга харьцангуй бага тооцоогоор үр дүнд хүрдэг.

Үндсэн тодорхойлолт ба тэмдэглэгээнүүд

n үл мэдэгдэгчтэй p шугаман тэгшитгэлийн системийг авч үзье. (p болон n тэнцүү байж болно.)

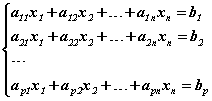
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.

request_quoteТусгай эрх авах

Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.

Холбоотой материалууд
Трапецид багтсан тойрог

  Нээгдсэн тоо: 6548 Төлбөртэй

Бодлогын нөхцөлд трапецид багтсан тойрогийн талаар дурдсан бол бодолтын санаагаа дараах шинжүүдийг үндэслэн хийж байгаарай. Үүнд:
1.
Дөрвөн өнцөгтийн эсрэг орших талуудын нийлбэр тэнцүү байхад л түүнд тойргийг багтааж болдог. Эндээс трапецид тойрог багтсан гэвэл түүний сууриудын нийлбэр хажуу талуудын нийлбэртэй тэнцүү байна.

AB+CD=AD+BC

Хавтгай

  Нээгдсэн тоо: 5425 Нийтийн

Хавтгайн геометрийг зөв ойлгохын суурь бол түүний үндсэн ухагдхуунуудыг маш сайн ойлгосон байх юм. Үндсэн ухагдхууныг ойлгоогүй бол геометрийн бодлого, асуултыг ойлгон зураг гаргах, асуудлыг шийдэх зэргийг давна гэдэг хэцүү. Хичээлээр хавтгай болон геометрийн дүрсүүд ухагдхууныг авч үзье.

Хавтгай.

Хавтгай гэдэг нь орон зайд тэгш, гөлгөр, бүх тал руу хязгааргүй тархсан гадургуу юм.

Зурагт хавтгайн хэсгийг харуулсан болно.

Тригнометрийн тэгшитгэлийн систем

  Нээгдсэн тоо: 3487 Нийтийн

Тригнометрийн тэгшитгэлийн системийг бодохдоо алгебрын / солих, орлуулах, хураах г.м / аргуудаас гадна тригнометрийн томьёо болон хувиргалтын аргуудыг ашиглана.

Жишээ 1

тэгшитгэлийн системийг бод.

Цэг хоорондын зай

  Нээгдсэн тоо: 832 Нийтийн

Координатийн шулуун дээрх хоёр цэгийн хоорондын зай нь тэдгээрийн координатуудын ялгаварын модултай тэнцүү. Үүнийг математикийн хэлээр буюу томьёогоор илэрхийлбэл

AB=|a-b|

юм. Энд A, B бол координатийн шулуун дээрх дурын хоёр цэг бөгөөд a, b нь тэдгээрийн координатууд.

Outlet компонент

Кодийн сайжруулалт /рефакторинг/ хичээлээр програмийн кодоо react -ийн зарчимд нийцүүлэн компонентод салгасан.…

Нээгдсэн тоо : 8

 
Хадгалагч (Memento)

Хадгалагч (Memento) хэв обьектын дотоод төлвийг түүний гадна гаргаж дараа нь хайрцаглалтын зарчмыг зөрчихгүйгээр обьектыг сэргээх боломжийг олгодог.

…

Нээгдсэн тоо : 18

 
Нэргүй арга

Делегаттай нэргүй арга нягт холбоотой. Нэргүй аргуудыг делегатийн хувийг үүсгэхэд ашигладаг.
Нэргүй аргуудын тодорхойлолт delegate түлхүүр үгээр…

Нээгдсэн тоо : 16

 
Урвуу матриц

Математикт харилцан урвуу тоонууд гэж бий. Ямар нэгэн тооны урвуу тоог олохдоо тухайн тоог сөрөг нэг зэрэг дэвшүүлээд…

Нээгдсэн тоо : 28

 
Кодийн сайжруулалт

Төсөлд react-router-dom санг оруулан чиглүүлэгчдийг бүртгүүлэн тохируулсан Санг суулган тохируулах хичээлээр бид хуудас…

Нээгдсэн тоо : 28

 
Хуваах

Хуваах нь нэг тоо нөгөө тоонд хэдэн удаа агуулагдаж буй тодорхойлох арифметикийн үйлдэл.
Хуваалтыг нэг бус удаа…

Нээгдсэн тоо : 28

 
Зуучлагч (Mediator)

Зуучлагч (Mediator) нь олон тооны обьектууд бие биетэйгээ холбоос үүсгэхгүйгээр харилцан ажиллах боломжийг хангах загварчлалын хэв юм. Ингэснээр…

Нээгдсэн тоо : 26

 
Делегатийн хэрэглээ

Делегатууд хичээлд ухагдхууны талаар дэлгэрэнгүй үзсэн ч жишээнүүд делегатийн хүчийг бүрэн харуулж чадахааргүй байсан.…

Нээгдсэн тоо : 38

 
Нэмэлт санг…

react програмд олон хуудас үүсгэн удирдахын тулд react -ийн бүрэлдхүүнд ордоггүй ч түүнтэй нягт холбоотой ажилладаг нэмэлт пакетийг…

Нээгдсэн тоо : 44

 
Энэ долоо хоногт
Бодлого 15.014

функц өгөгдөв.

  1. f(x) функцын x0=5 абсцисстай M цэгт татсан шүргэгч шулууны тэгшитгэл
  2. f(x) функцын график, дээрх шүргэгч шулуун болон координатын тэнхлэгүүдээр хүрээлэгдсэн дүрсийн талбай  
  3. f(x) функцын графикийг M цэгт шүргэх, төв нь OX (абсцисс) тэнхлэг дээр орших тойргийн тэгшитгэл

Нээгдсэн тоо : 2767

 
Бодлого 2.094

илэрхийллийн a=36,7 тэнцүү байх утгыг ол.

Нээгдсэн тоо : 657

 
Бодлого 3.094

a ба b нь 3x2-x-1=0 тэгшитгэлийн шийдүүдтэй тэнцүү бол илэрхийллийн утгыг ол.

Нээгдсэн тоо : 693

 
© 2014 Зохиогчийн эрхээр хамгаалагдсан. Холбогдох - 96655195