Математикийн бодлого бодоход томьёонууд чухал үүрэгтэй гэдгийг бүгд мэддэг. Ерөнхий боловсролын сургуулийн математикийн хичээлийн агуулгад хамаарагдах томьёонууд нилээд олон тооны боловч бодлого бодоход эдгээрийн цөөн хэсгийг нь илүү ихээр ашигладаг. Жишээлбэл үржүүлэхийг хураангуй томьёонууд, квадрат тэгшитгэлийн шийдийг олох, Виетийн тоерем, прогрессийн томьёонууд, Пифагор, синус, косинусын теоремууд гээд бараг тогтмол ашигладаг томьёонуудыг дурдаж болно.
Сурагчид томьёонуудыг мэдээд байгаа хирнээ түүнийг бодлогод ашиглах тал дээр нилээд сул байдаг. Энэ нь дадлага дутсан эсхүл томьёогоо ойлголгүй шууд цээжилсэнтэй холбоотой. Дадлага дутаж байгаа бол асуудал гайгуй. Харин ойлгохгүйгээр цээжлэх бол асуудалтай. Бодлогод томьёог хэрэглэж чадахгүй байгаагийн шалтгаан аль нь болохыг та өөрөө ч олох боломжтой. Томьёогоо мэдэж байна уу. Тэгвэл нэг бодлогыг өөрөө бодох гээд үз. Чадахгүй бол бодолтыг нь хар. Энэ мэтээр 7 хоног ажиллаад үз. Долоо хоногийн дараа мэддэг томьёогоо хүндрэлгүй ашиглаж чаддаг болчихвол эхний шалтгаан байж. Харин долоо хоноход үр дүн муутай байвал хоёрдахь шалтгаан байх талтай. Гэхдээ мэдээж таны оролдлого зүтгэл их үүрэгтэй. Оргүйгээс охинтой гэдэг шиг та ядахдаа томьёогоо мэдэж байгаа шүү дээ.
Автоматаар цээжилсэн томьёог мартах нь амарахн байдаг. Тэгэхлээр томьёо хэрхэн зөв тогтоох вэ?
Зарим сурагчдаас нийлбэрийн квадратын томьёо гэж асуухад хариулж мэдэхгүй мөртлөө (a+b)2 гэж асуухад 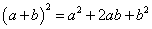 гээд шууд хэлж байгаа юм. Косинусын теоремыг
гээд шууд хэлж байгаа юм. Косинусын теоремыг 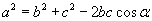 гээд томьёололыг хэлээд байгаа мөртлөө үүнийгээ тайлбарлаж чадахгүй байх жишээтэй. Энэ бол томьёог автоматаар цээжилсний шинж. Үүнийг цээжилж чадаж байна гэдэг бас боломжийн.
гээд томьёололыг хэлээд байгаа мөртлөө үүнийгээ тайлбарлаж чадахгүй байх жишээтэй. Энэ бол томьёог автоматаар цээжилсний шинж. Үүнийг цээжилж чадаж байна гэдэг бас боломжийн.
Томьёог хэлбэрээр нь цээжлэх биш тодорхойлолтоор нь тогтоох хэрэгтэй.
Дээрх хоёр томьёог үгээр тодорхойлбол
- Нийлбэрийн квадрат нь 1-р нэмэгдхүүний квадрат дээр нэмэгдхүүнүүдийн үржвэрийг хоёроор үржүүлэн нэмээд 2-р нэмэгдхүүний квадратыг нэмсэнтэй тэнцүү.
- Косинусын теорем бол дурын гурвалжны хоёр тал ба тэдгээрийн хоорондох өнцөг мэдэгдэж байвал гуравдагч талын квадрат нь мэдэгдэж байгаа талуудын квадратуудын нийлбэрээс талуудын үржвэрийг хоёр дахин аваад тэдгээрийн хоорондох өнцгийн косинусаар үржүүлсэн үржвэрийг хассантай тэнцүү.
Яг ийм байдлаар бүх томьёоны тодорхойлолтыг мэддэг байх хэрэгтэй. Ингэж тогтоовол 1-рт амархан тогтооно, 2-рт мартах нь удаан, 3-рт бодлогод ашиглаж сурахад хөнгөн байдаг. Томьёог тодорхойлолтоор тогтоох шалтгааныг тайлбарлая.
- Практикт a тэнцүү тэд, b тэнцүү тэд гээд (a+b)2 ол гэсэн бодлого бараг тохиолдохгүй. Ийм жишээнүүдийг зөвхөн сурах бичигт л тухайн сэдвийг ойлгуулахад зориулан оруулдаг. Түүнээс шалгалт, шүүлэгт ийм хэлбэрийн бодлого ирэх нь бараг үгүй. Илэрхийлэл эмхэтгэх, тэгшитгэл, тэнцэтгэл биш бодох үндсэн арга нь томьёонуудыг задгай байдлаас хураангуй бичлэгт шилжүүлэх байдаг. Жишээ нь илэрхийллээс бүтэн квадрат эсхүл куб ялгах гэх мэтээр. Иймд томьёонуудыг хоёр тал руу нь чөлөөтэй шилжүүлж чаддаг байх хэрэгтэй. Өөрөөр хэлбэл задгайгаас хураангуйд, хураангуйгаас задгайд гэсэн үг. Энд бас л томьёоны тодорхойлолт л тус болно.
- Томьёоны илэрхийлэлд орж байгаа гишүүд /a, b, c, өнцөг гэх мэт/ бодлогын нөхцлөөс шалтгаалан язгуур доорх тоо, логарифм, тригнометрийн функц гээд янз бүр байж болно. Энэ үед нөгөө дасал болсон a, b, c -нууд байхгүй тул автомат цээжилсэн сурагчид хүнд байдалд ордог. Тодорхойлолтыг мэдэж байвал үүнд сандрах зүйлгүй. Жишээ нь нэмэгдхүүн эсхүл гурвалжны талууд ямарч байдлаар бүр функц байдлаар ч өгөгдөж болно.
- Геометрийн бодлогууд зургаар өгөгдөх нь элбэг. Тэнд a нь энэ, b нь энэ гэж заахгүй. Зүгээр л зураг өгөгдөнө. Энэ үед автомат цээжилсэн томьёо бүр ажиллахгүй.
- Үржүүлэхийн хураангуй томьёо, квадрат тэгштгэлийн шийдийг олох зэрэгт автоматаар цээжлээд ашиглаад байж болох талтай ч дүрс нь багахан өөрчлөгдөхөд л нам зогсох аюултай. Харин геометр, тригнометр гэх мэтийн байгуулалттай холбоотой томьёонуудыг заавал тодорхойлолтоор нь мэддэг байх хэрэгтэй
Энэ мэтээр олон тохиолдолыг дурдаж болно. Гэхдээ бүх томьёог тодорхойлолтоор нь ойлгож авна гэвэл бас боломжгүй. Жишээ нь уламжлал, интегралуудын үндсэн жагсаалтыг шууд цээжлэхээс өөр аргагүй. Учир нь ЕБС-д математик анализын эхлэлтэй дөнгөж танилцах хэмжээнд үздэг тул нарийн ойлгох боломжгүй. Энд цөөн хэдэн гол томьёонууд байдаг. Харин ЭЕШ -д зарим нэгэн томьёонуудыг хуудас дээр оруулан өгдөг нь их сайн зүйл. Хүн бүр бүх томьёог санаж байх албагүй шүү дээ.
Сайтын бодлогуудын бодолтуудад ашиглагдаж байгаа томьёонуудыг шууд оруулан өгсөн байгаа болохоор та бодолтыг үзэхдээ томьёонуудыг харсаар тэдгээрийг тогтоохын зэрэгцээ ямар төрлийн бодлогод ямар томьёонуудыг ашиглахыг сурах юм.





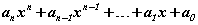 гэсэн ерөнхий хэлбэртэй байдаг. n=1 бол
гэсэн ерөнхий хэлбэртэй байдаг. n=1 бол  функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.