Илэрхийллийг үржигдхүүнд задлах 4 дэх аргад квадрат гурван гишүүнтийг задлах ордог тухай бид Бодлого бодож сурах нь I хичээлд дурдсан байгаа. Бид үржүүлэхийн хураангуй томьёог ашиглан үржигдхүүнд задлах хичээлийн эцэст x²-6x+8 илэрхийллийг бүлэглэх аргыг ашиглан үржигдхүүнд задалсан. Ийм төрлийн илэрхийллийг хэрхэн үржигдхүүнд задлах талаар энэ хичээлээр авч үзэх болно.

Квадрат гурван гишүүнтийг үржигдхүүнд задлах

Ямар нэгэн хувьсагчийн хоёрдугаар эрэмбийг агуулсан олон гишүүнтийг квадрат гурван гишүүнт гэдэг. Квадрат гурван гишүүнт

ax²+bx+c

ерөнхий хэрбэртэй байна. Энд a, b, c нь ямар нэгэн тодорхой тоонууд харин x нь янз бүрийн утгуудыг авч болно. x -ийн утгаас хамааран гурван гишүүнт төрөл бүрийн утгатай байх боломжтой гэдэг нь ойлгомжтой. Иймээс x-ийг олон гишүүнтийн аргумент гэж нэрлэдэг. Үүнийг жишээгээр x²-3x+2 олон гишүүнт дээр авч үзье. Олон гишүүнтийг y гэж тэмдэглэвэл y=x²-3x+2 гэж бичиж болно. Одоо x -д утгуудыг өгөхөд олон гишүүнтийн авч байгаа утгуудыг хүснэгтээр үзүүлбэл

Хүснэгтээс харвал x-ийн 1 ба 2 утганд олон гишүүнтийн утга тэг болсон. Эндээс доорх тодорхойлолт гарч ирнэ.

Гурван гишүүнтийн утгыг тэгтэй тэнцүүлэх аргументын утгуудыг түүний шийдүүд гэнэ.

Тодорхойлолтын дагуу бидний жишээгээр авсан гурван гишүүнтийн шийдүүд 1, 2 болж таарна. Эдгээр утгуудад олон гишүүнтийн утга тэгтэй тэнцүү болсон.
Квадрат гурван гишүүнтийг үржигдхүүнд задлах арга нь яг энэ шийдүүдийг ашигладаг. Олон гишүүнтийн шийдийг олохын тулд түүнийг тэгтэй тэнцүүлэн x -ийн утгыг хайна. Өөрөөр хэлбэл олон гишүүнтийг тэг утгатай байлгах аргументын утгыг олохын тулд ax²+bx+c=0 тэгшитгэлийг бодно гэсэн үг.Квадрат тэгшитгэлийг бодох аргаас түүний дискриминантаас хамааран тэгшитгэл хоёр өөр эсхүл хоёр ижил эсхүл шийдгүй байж болдог гэдгийг бид мэднэ. Энэ нь ч квадрат гурван гишүүнтэд бас хамаарагдана. Гурван гишүүнт бас хоёр өөр эсхүл хоёр ижил эсхүл шийдгүй байж болно. Иймээс тэгшитгэлийн дискриминантыг бас гурван гишүүнтийн дискриминант гэж нэрлэдэг.

Квадрат гурван гишүүнтийг задлах.

x²+px+q хэлбэрийн гурван гишүүнтийг үржигдхүүнд задлах.

y=x²+px+q гурван гишүүнт x₁, x₂ гэсэн шийдтэй гэж үзье. Тэгвэл x₁, x₂ нь x²+px+q=0 тэгшитгэлийн шийд болох ёстой. Нөгөө талаас Виетийн теоремоор x₁+x₂=-p; x₁·x₂=q байна. Эндээс -(x₁+x₂)=p; x₁·x₂=q болох бөгөөд утгуудыг гурван гишүүнд тавин хувиргалтыг хийвэл

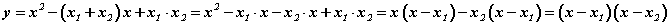гарна. Ингээд x²+px+q хэлбэрийн гурван гишүүнт 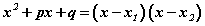гэж үржигдхүүнд задарлаа. Эндээс x²+px+q хэлбэрийн гурван гишүүнт шийдүүдтэй бол олон гишүүнт аргумент болон шийдүүдийн ялгаваруудын үржвэр хэлбэрээр үржигдхүүнд задарна гэсэн тодорхойлолтонд хүрлээ.

Жишээ
Бодлого бодож сурах нь III хичээлийн төгсгөлд үзсэн x²-6x+8 илэрхийллийг авч үзье.

Бодолт
Илэрхийллийг бид бүлэглэх аргаар үржигдхүүнд задалж байсан. Одоо илэрхийллийн дээрх аргаар үржигдхүүнд задлая. Гурван гишүүнтийн шийдийг олохын тулд x²-6x+8=0 тэгшитгэлийг бодох хэрэгтэй. Тэгшитгэлийг бодвол x₁=2; x₂=4 гэсэн шийдүүд олдоно. Тэгвэл өгөгдсөн илэрхийлэл x²-6x+8=(x-2)(x-4) байдлаар үржигдхүүнд задарна.

ax²+bx+c хэлбэрийн гурван гишүүнтийг үржигдхүүнд задлах.

Гурван гишүүнтийг y=ax²+bx+c гэж бичээд a≠0 , x₁, x₂ гэсэн шийдтэй гэж үзье. Гурван гишүүнтээс a -г хаалтны өмнө гаргавал. 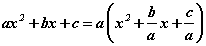[1] хэлбэртэй болно. x₁, x₂ нь ax²+bx+c=0 тэгшитгэлийн шийд тул 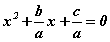тэгшитгэлийн шийд бас болж чадна. Эндээс өмнөх тохиолдолын дагуу гурван гишүүнт 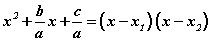гэж үржигдхүүнд задарна. Үүнийг [1] -д орлуулбал

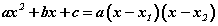гарна. Эндээс шийд бүхий ax²+bx+c хэлбэрийн гурван гишүүнт нь x² -ийн коэффициент, аргумент болон шийдүүдийн ялгаваруудын үржвэр хэлбэрээр гурван үржигдхүүн болон задардаг байна.

Бодлого 2.058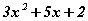      
илэрхийллийг үржигдхүүнд задал

Бодолт

Бодлого 2.059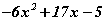
илэрхийллийг үржигдхүүнд задал

Бодолт