Олон бодлого бодоод байвал математикт сайжирна гэсэн яриа хүмүүсийн дунд өргөн тархсан байдаг. Бодлого ихээр бодох нь техник талаасаа сайн нөлөөтэй болохоос математикийг ойлгодог болгоно гэдэг эргэлзээтэй. Онолын мэдлэгтэй байх нь ямарч хичээлийн хувьд үндсэн асуудал. Онолгүйгээр хол явахгүй гэж ярьдаг үүнийг хэлж байгаа юм. Энэ удаад Виетийн теоремийн тухай үргэлжлүүлэн авч үзье. Теорем гэдэг нь баталгаа шаардлагатай тодорхойлолт буюу нотолгоо. Өмнөх Виетийн теорем хичээлд жишээ болгон авч үзсэн гурван тэгшитгэлд теорем ажиллаж байгаа ч ямарч тэгшитгэлд адилхан ажиллана гэдгийг батлах хэрэгтэй. Теоремийг нээн олсон математикчид өөрсдөө батлаад түүнийг нь бусад нь хүлээн зөвшөөрсөн учраас математикт теоремоор бүртгэсэн хэрэг. Өнөөг хүртэл жишээ нь Фермагийн их теорем гэдэг нотолгоо батлагдаагүй, олон тооны интегралууд бодогдоогүй байсаар л байгаа. Хүн өөрийн дэвшүүлсэн санаа, нотолгоог баталснаар тэр нь теорем болно.
Теорем болгоны баталгааг заавал мэдэх албагүй ч сонирхолтой байх үүднээс Виетийн теоремийн баталгааг харцгаая. x2 + bx + c = 0 бүрэн квадрат тэгшитгэл өгөгдсөн гэе. Хэрвээ түүний дискриминант тэгээс их бол тэгшитгэл хоёр шийдтэй байх бөгөөд тэдгээрийн нийлбэр тэгшитгэлийн 1 -р эрэмбийн үл мэдэгдэгчийн коэффициентийг сөрөг тэмдэгтэй авсантай харин үржвэр нь тэгшитгэлийн сул гишүүнтэй тэнцүү. Математикийн бичлэгээр x2 + bx + c = 0 бүрэн квадрат тэгшитгэлийн шийдийг x1, x2 гэвэл 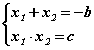
тэнцлүүдийн систем биелнэ. Дээрх тэнцэл зөв эсэхийг батлая. Квадрат тэгшитгэлийн шийдийг олох
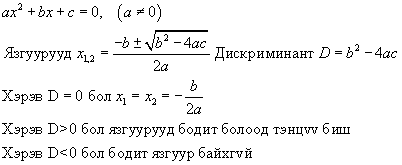 томьёоны дагуу тэгшитгэл
томьёоны дагуу тэгшитгэл 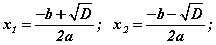 шийдүүдтэй. x1+x2 нийлбэрийг олъё. x2+bx+c=0 бүрэн квадрат тэгшитгэлийн хувьд 2 -р эрэмбийн үл мэдэгдэгчийн коэффициент 1 гэдгийг сануулъя. Өөр хэлбэл a=1 гэсэн үг. Нийлбэрийг олбол
шийдүүдтэй. x1+x2 нийлбэрийг олъё. x2+bx+c=0 бүрэн квадрат тэгшитгэлийн хувьд 2 -р эрэмбийн үл мэдэгдэгчийн коэффициент 1 гэдгийг сануулъя. Өөр хэлбэл a=1 гэсэн үг. Нийлбэрийг олбол 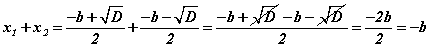 гэж гарснаар x1+x2=-b гэдэг нь батлагдлаа. Одоо шийдүүдийг хооронд нь үржүүлбэл
гэж гарснаар x1+x2=-b гэдэг нь батлагдлаа. Одоо шийдүүдийг хооронд нь үржүүлбэл
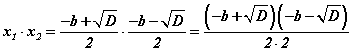 болно. Хүртвэрт квадратуудын ялгаварын
болно. Хүртвэрт квадратуудын ялгаварын 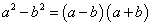 томьёог хэрэглэвэл
томьёог хэрэглэвэл 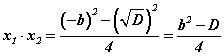 болно. Квадрат тэгшитгэлийн шийдийг олох томьёоноос дискриминант b2-4ac -тэй тэнцүү гэдгийг мэдэх тул түүнийг сүүлийн бутархайд тавивал
болно. Квадрат тэгшитгэлийн шийдийг олох томьёоноос дискриминант b2-4ac -тэй тэнцүү гэдгийг мэдэх тул түүнийг сүүлийн бутархайд тавивал 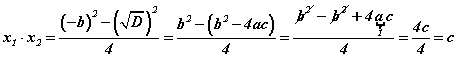 гэж гарснаар системийн 2 -р тэнцэл биелснээр теорем батлагдлаа.
гэж гарснаар системийн 2 -р тэнцэл биелснээр теорем батлагдлаа.
Виетийн теоремийн тонгоруу теорем.
Теоремийн нэрийг жаахан буруу нэрлэсэн байж магадгүй. Бүрэн квадрат тэгшитгэлийн шийдүүдийн нийлбэр, үржвэрийн тэнцлийн системийг гаргасны дараа тэгшитгэлд тохирох шийдүүдийн сонголтыг хийх болдог. Энэ үед л Виетийн теоремийн тонгоруу теоремийг ашигладаг. Теоремийг тодорхойлбол:
Хэрвээ x1, x2 тоонуудын нийлбэр x2+bx+c=0 бүрэн квадрат тэгшитгэлийн 1 -р эрэмбийн үл мэдэгдэгчийн коэффициентийг сөрөг тэмдэгтэй авсантай харин үржвэр нь тэгшитгэлийн сул гишүүнтэй тэнцүү бол x1, x2 тоонууд x2+bx+c=0 тэгшитгэлийн шийд болно.
Теоремийг x2-6x+8=0 тэгшитгэл дээр авч үзье. Тэгшитгэлд Виетийн теоремийг бичвэл 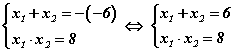 систем үүснэ. Одоо системийг хангах тоонуудыг олчихвол тэдгээр нь Виетийн теоремийн тонгоруу теоремоор анхдагч тэгшитгэлийн шийд болох ёстой. Тэгшитгэлийн шийдүүдийг үржвэрээс сонгох нь илүү амар байдаг тул хоёрдахь тэнцлийг хангах тоонуудыг сонгоё.
систем үүснэ. Одоо системийг хангах тоонуудыг олчихвол тэдгээр нь Виетийн теоремийн тонгоруу теоремоор анхдагч тэгшитгэлийн шийд болох ёстой. Тэгшитгэлийн шийдүүдийг үржвэрээс сонгох нь илүү амар байдаг тул хоёрдахь тэнцлийг хангах тоонуудыг сонгоё. 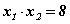 тэнцлийг 1·8=8, 2·4=8 гэдгээс 1; 8; 2; 4 тоонууд хангана. Гэхдээ эдгээр тоонууд 1 -р тэнцлийг хангасан тохиолдолд тэгшитгэлийн шийд болох ёстой учраас шалгах хэрэгтэй. 1+8≠6; 2+4=6 гэдгээс 2 болон 4 тоонууд тэгшитгэлийн шийд гэдэг нь харагдана. Эндээс x1=2; x2=4 гэж гарна.
тэнцлийг 1·8=8, 2·4=8 гэдгээс 1; 8; 2; 4 тоонууд хангана. Гэхдээ эдгээр тоонууд 1 -р тэнцлийг хангасан тохиолдолд тэгшитгэлийн шийд болох ёстой учраас шалгах хэрэгтэй. 1+8≠6; 2+4=6 гэдгээс 2 болон 4 тоонууд тэгшитгэлийн шийд гэдэг нь харагдана. Эндээс x1=2; x2=4 гэж гарна.
Тонгоруу теоремд бусад теоремуудын адилаар баталгаа шаардана. Теоремийг батлая. Тооцоонд эвтэйхэн байлгах үүднээс тоонуудыг m, n гэж үзье. Теорем ёсоор m, n тоонууд 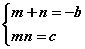 системийг хангаж байвал x2+bx+c=0 тэгшитгэлийн шийдүүд байх ёстой. m, n -ээр тэгшитгэлийн b, c коэффициентүүд илэрхийлэгдэж байгаа учраас m, n нь тэгшитгэлийн шийд мөн эсэхийг шалгахын тулд тэдгээрийг тэгшитгэлд тавин тооцоог хийе. Системийн эхний тэнцэл b коэффициентийг сөрөг тэмдэгтэй авсанг b=-m-n болговол тооцоонд ойлгомжтой. Ингээд x1=m гэж үзээд түүнийг тэгшитгэлд тавин тооцвол
системийг хангаж байвал x2+bx+c=0 тэгшитгэлийн шийдүүд байх ёстой. m, n -ээр тэгшитгэлийн b, c коэффициентүүд илэрхийлэгдэж байгаа учраас m, n нь тэгшитгэлийн шийд мөн эсэхийг шалгахын тулд тэдгээрийг тэгшитгэлд тавин тооцоог хийе. Системийн эхний тэнцэл b коэффициентийг сөрөг тэмдэгтэй авсанг b=-m-n болговол тооцоонд ойлгомжтой. Ингээд x1=m гэж үзээд түүнийг тэгшитгэлд тавин тооцвол 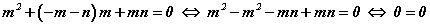 болсноор m тэгшитгэлийн шийд гэдэг нь батлагдана. x2=n гэж үзээд өмнөхийн адилаар тэгшитгэлд тавин тооцвол (тооцоог танд үлдээе) m, n нь тэгшитгэлийн шийдүүд гэдэг нь батлагдсанаар теорем батлагдана. Теоремийг ашиглахыг жишээгээр харцгаая.
болсноор m тэгшитгэлийн шийд гэдэг нь батлагдана. x2=n гэж үзээд өмнөхийн адилаар тэгшитгэлд тавин тооцвол (тооцоог танд үлдээе) m, n нь тэгшитгэлийн шийдүүд гэдэг нь батлагдсанаар теорем батлагдана. Теоремийг ашиглахыг жишээгээр харцгаая.
Жишээ
x2+16x+15=0 тэгшитгэлийг бод.
Бодолт
Тэгшитгэлийн шийдүүдийг x1, x2 гэе. Тэгвэл Виетийн тонгоруу теоремоор 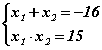 систем биелэх ёстой. Хоёр тооны үржвэр эерэг гарахын тулд нэг бол тоонууд хоёулаа эерэг эсхүл хоёулаа сөрөг байх ёстой. Эдгээр тоонуудын нийлбэр -16 гэдгээс тоонууд эерэг байх боломжгүй хоёулаа сөрөг байх ёстой нь гарна. 15 -ыг -1, -15 эсхүл -3, -5 тоонуудын үржвэрээр гаргаж болно. Эдгээрээс -1, -15 тоонууд системийн 1 -р тэгшитгэлийг хангах учраас Виетийн тонгоруу теоремоор -1, -15 тоонууд өгөгдсөн тэгшитгэлийн шийд болно.
систем биелэх ёстой. Хоёр тооны үржвэр эерэг гарахын тулд нэг бол тоонууд хоёулаа эерэг эсхүл хоёулаа сөрөг байх ёстой. Эдгээр тоонуудын нийлбэр -16 гэдгээс тоонууд эерэг байх боломжгүй хоёулаа сөрөг байх ёстой нь гарна. 15 -ыг -1, -15 эсхүл -3, -5 тоонуудын үржвэрээр гаргаж болно. Эдгээрээс -1, -15 тоонууд системийн 1 -р тэгшитгэлийг хангах учраас Виетийн тонгоруу теоремоор -1, -15 тоонууд өгөгдсөн тэгшитгэлийн шийд болно.
Жишээ
x2-10x-39=0 тэгшитгэлийг Виетийн тонгоруу теоремоор бод.
Бодолт
Виетийн тонгоруу теоремоор нийлбэр, үржвэрүүд нь 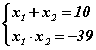 системийг хангах x1, x2 тоонууд тэгшитгэлийн шийд байх ёстой. Үржвэр сөрөг байна гэдэг нь аль нэг тоо нь сөрөг гэдгийг заана. -39 тоо 13, -3 эсхүл -13, 3 тоонуудын үржвэрээр гарах бөгөөд тэдгээрийн нийлбэр 10 тай тэнцэх нөхцлийг 13, -3 тоонууд хангана. Иймээс Виетийн тонгоруу теоремоор өгөгдсөн тэгшитгэлийн шийдүүд x1=13, x2=-3 гэж гарна.
системийг хангах x1, x2 тоонууд тэгшитгэлийн шийд байх ёстой. Үржвэр сөрөг байна гэдэг нь аль нэг тоо нь сөрөг гэдгийг заана. -39 тоо 13, -3 эсхүл -13, 3 тоонуудын үржвэрээр гарах бөгөөд тэдгээрийн нийлбэр 10 тай тэнцэх нөхцлийг 13, -3 тоонууд хангана. Иймээс Виетийн тонгоруу теоремоор өгөгдсөн тэгшитгэлийн шийдүүд x1=13, x2=-3 гэж гарна.
Жишээ
x2+bx+45=0 тэгшитгэлийн эхний шийд 15 бол хоёрдахь шийд болон b коэффициетийг ол.
Бодолт
Виетийн теоремоор эмхэтгэсэн квадрат тэгшитгэлийн шийдүүдийн үржвэр x1·x2=45 сул гишүүнтэй тэнцүү гэдгээс 15·x2=45 тэгшитгэл үүсэн эндээс x2=3 гэж гарна. Нөгөө талаас x1+x2=-b тэй тэнцүү байх ёстой. Шийдүүдийг тэгшитгэлд тавин тооцвол 15+3=-b буюу b=-18 гэж гарна.
Бүрэн буюу эмхэтгээгүй квадрат тэгшитгэлийн Виетийн теорем
Виетийн теорем зөвхөн эмхэтгэсэн квадрат тэгшитгэлд ажилладаг гэж ойлгож болохгүй. Жишээ нь ax2+bx+c=0 бүрэн квадрат тэгшитгэл байлаа гэе. Виетийн теоремийг тэгшитгэлд хэрэглэхийн тулд квадрат зэрэгтэй үл мэдэгдэгчийн коэффициентод тэгшитгэлийн хоёр талыг хуваавал 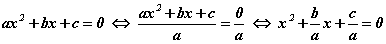 эмхэтгэсэн квадрат тэгшитгэл үүснэ. Одоо тэгшитгэлийн 1 -р эрэмбийн үл мэдэгдэгчийн коэффициент b/a харин сул гишүүн c/a болсон. Тэгшитгэлд Виетийн теоремийг бичвэл
эмхэтгэсэн квадрат тэгшитгэл үүснэ. Одоо тэгшитгэлийн 1 -р эрэмбийн үл мэдэгдэгчийн коэффициент b/a харин сул гишүүн c/a болсон. Тэгшитгэлд Виетийн теоремийг бичвэл 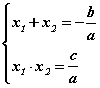 хэлбэртэй болно.
хэлбэртэй болно.
Жишээ
3x2-7x+2=0 тэгшитгэлийг бод.;
Бодолт
Эхлээд тэгшитгэлийг эмхэтгэсэн хэлбэрт оруулъя. Үүний тулд квадрат зэрэгтэй үл мэдэгдэгчийн коэффициентод тэгшитгэлийн хоёр талыг хуваавал 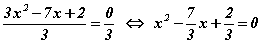 тэгшитгэл үүсэх бөгөөд Виетийн теоремийг бичвэл
тэгшитгэл үүсэх бөгөөд Виетийн теоремийг бичвэл 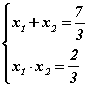 систем үүснэ. Сонгох аргаар системийг 2, 1/3 тоонууд хангана гэдгийг тодорхойлон тэгшитгэлийг бодно.
систем үүснэ. Сонгох аргаар системийг 2, 1/3 тоонууд хангана гэдгийг тодорхойлон тэгшитгэлийг бодно.
Жич: Квадрат тэгшитгэлийн шийдийг стандарт томьёонуудаар олох нь амар байдаг тул Виетийн теоремийг тийм өргөн ашиглаад байдаггүй. Гэхдээ зарим бодлогод Виетийн теорем хэрэг болох үе бий.
Жишээ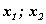 нь
нь 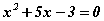 тэгшитгэлийн шийдүүд бол
тэгшитгэлийн шийдүүд бол 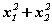 -ийг ол.
-ийг ол.
Бодолт
Бодлогыг стандарт аргаар шийдэх гэвэл нилээд их тооцоо хийх хэрэг гарна. Үүний оронд тэгшитгэлд Виетийн теорем бичвэл 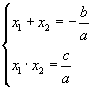 систем биелэх ёстой. Теоремийг ашиглахын тулд
систем биелэх ёстой. Теоремийг ашиглахын тулд 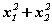 илэрхийлэлд багахан хувиргалт хийгээд
илэрхийлэлд багахан хувиргалт хийгээд 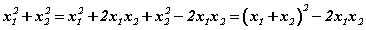 хэлбэрт оруулбал теорем ёсоор
хэлбэрт оруулбал теорем ёсоор 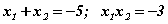 байх ёстой. Тэгвэл
байх ёстой. Тэгвэл 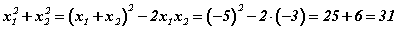 гэдэг нь амархан харагдана. Бодлогыг стандарт аргаар өөрсдөө шийдээрэй.
гэдэг нь амархан харагдана. Бодлогыг стандарт аргаар өөрсдөө шийдээрэй.
Виетийн теоремийг мэдэхгүй бол та хичнээнч квадрат тэгшитгэл бодсон байлаа ч сүүлийн бодлогод ийм техникийг ашиглаж чадахгүй стандарт аргаар л шийдэхэд хүрнэ. Иймээс л математикийг ойлгохын тулд онолыг сайтар судлахыг зөвлөөд байгаа хэрэг.





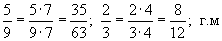
 задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.