Гурвалжны гайхамшигт цэгүүдээс сурагчдын хамгийн бага мэдээлэлтэй байдаг нь орто төв, орто гурвалжин байдаг. Гэтэл элсэлтийн шалгалт дээр ийм төрлийн бодлогууд ирэх тохиолдол байна. Иймээс энэ хичээлээр гурвалжны орто төв гэж юуг хэлэх түүнийг бодлогод хэрхэн ашиглахыг элсэлтийн ерөнхий шалгалтанд ирж байсан бодлогууд дээр тайлбарлах болно.
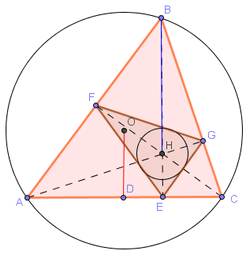Ямарч гурвалжны хувьд түүний өндрүүд эсхүл тэдгээрийн үргэлжлэл нь нэг цэгт огтлолцдог. Энэ цэгийг орто төв гэж нэрлэдэг. Орто төвийн байрлал гурвалжны төрлөөс хамаардаг.
- Хурц өнцөгт гурвалжны орто төв гурвалжин дотроо байрлана.
- Мохоо өнцөгт гурвалжинд орто төв гурвалжны гадна байршина.
- Тэгш өнцөгт гурвалжинд орто төв нь тэгш өнцгийн орой дээр байрладаг.
Орто төвийг ихэвхичлэн H үсгээр тэмдэглэх бөгөөд дараах шинжүүдтэй
- Гурвалжны гурван орой (A,B,C) болон орто төв H дөрвөн цэгийн аль нь ч бусад гурван цэгээр байгуулсан гурвалжны орто төв нь болдог. Заримдаа ийм дөрвөн цэгийг орто төвийн систем ч гэж нэрлэдэг.
- Орто төвийн системийн дурын 3 цэгийг дайран өнгөрөх тойргуудын радиусууд тэнцүү
- ABC гурвалжны өндрүүдийн тал дээр буусан цэгүүдээр үүсэх гурвалжинг (FGE) орто гурвалжин гэнэ.
- Хурц өнцөгт ABC гурвалжны орто төв H нь FGE орто гурвалжинд багтсан тойргийн төв болдог.
- O -г ABC гурвалжинг багтаасан тойргийн төв гэвэл
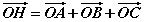тэнцэл биелэнэ. 
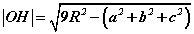Энд R- ABC гурвалжинг багтаасан тойргийн радиус, a,b,c - гурвалжны талууд- Гурвалжны дурын оройгоос түүний орто төв хүртлэх зай нь оройн эсрэг талаас гурвалжинг багтаасан тойргийн төв хүртэлх зайнаас хоёр дахин их байдаг.
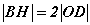
Сүүлийн харьцаа маш чухал харьцаа тул тогтоож аваарай. Үүнийг баталъя.
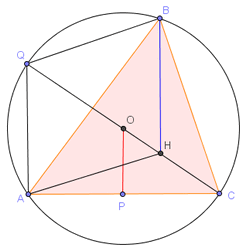
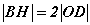тэнцлийн баталгааг үзүүлж байгаа нь 1-рт харьцаа нь их чухал 2-рт баталгааг хийж сурдаггүй юм гэхэд баталгаанд ашиглаж байгаа ухагдхуун нь геометрийн баталгаа шаардахгүй суурь ойлголтууд байдаг тул эдгээрийг ойлгон тогтоон авахад их хэрэгтэй. Бодлого бодохдоо бид теорем, лемм, суурь ойлголтуудаар л үндсэн гаргалгааг хийх болдог. Баталгааг хийж чадахгүй гээд орхиж болохгүй. Сайн уншаад ойлгохыг хичээ. Тогтоож авах нь гол биш хэрхэн гаргалгаа хийж байгааг сурахыг хичээгээрэй.
CO шулуун багтаасан тойргийг Q цэгт огтлоно гэж үзье. зургийг хар. CQ нь диаметр тул QAP өнцөг 90 буюу тэгш өнцөг. Харин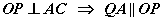 
байна. AOC гурвалжин адил хажуут OP нь түүний өндөр тул |AP|=|PC| болох тул OP нь CQA гурвалжны дундаж шугам 
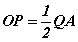болох нь. 
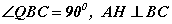гэдгээс (яагаад гэдгийг өөрсдөө батлаарай) QB||AH байна. Нөгөө талаас 
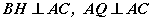учраас AQ||BH болж таарна. Эндээс AQBH нь паралелграмм гэдэг нь батлагдах бөгөөд өөрөөр хэлбэл AQ=BH гэсэн үг. Ингээд 
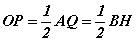болсноор харьцаа батлагдлаа.
Одоо орто төвтэй холбогдолтой бодлогын жишээ авч үзье.
Бодлого 9.026 ЕШ 2013 А-21
ABC гурвалжны A ба C оройн өндрүүд H цэгт огтлолцоно. Хэрэв ABC гурвалжныг багтаасан тойргийн радиус 4 нэгж ба 
бол |BH|=?
Бодлого 9.036 ЕШ 2008 A-12
ABC гурвалжны хувьд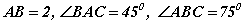 
ба орто төв нь H бол AH хэрчмийн уртыг ол.
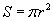томьёогоор илэрхийлэгдэнэ; Хоёр хувьсагчийн функционал хамаарал хэсэгт авч үзсэн дээш шидэгдсэн биеийн хүрэх өндөр h, нийт хугацаа T хоёрын хамаарал гэх мэт. Агаарын эсэргүүцэл, дэлхийн таталтын хүч өндрөөс хамаардаг зэргийг тооцоогүй учраас энэ нь ойролцоо томьёо юм. Функционал хамааралыг томьёогоор илэрхийлэх боломжгүй эсвэл томьёо нь тооцоо хийхэд тохиромж муутай байх тохиолдол бас байдаг. Ийм үед функцыг хүснэгт эсвэл графикаар үзүүлдэг.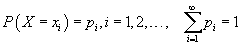
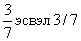
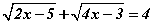тэгшитгэл бод.
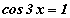тэгшитгэл бод.
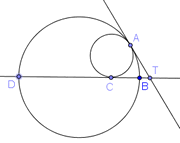Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.