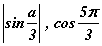 тоонууд гурвалжины талууд болдог байх α -г ольё.
тоонууд гурвалжины талууд болдог байх α -г ольё.
- Тэгвэл
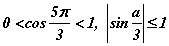 гэдгээс
гэдгээс 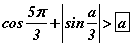 нөхцөл биелэхэд л хангалттай.
нөхцөл биелэхэд л хангалттай. - Иймд
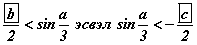 байна.
байна. - Эндээс
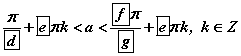 байна.
байна.
Бодолт
- Гурвалжны хоёр талын нийлбэр үлдсэн талаасаа их байдаг. Иймээс
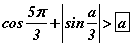 биелэх ёстой. Косинус, синус функцуудын утгын муж -1 -ээс 1 -ийн хооронд байдаг ч тоонууд гурвалжны талууд болдог гэсэн учраас нэмэх утгуудтай байх ёстой гэдгээс
биелэх ёстой. Косинус, синус функцуудын утгын муж -1 -ээс 1 -ийн хооронд байдаг ч тоонууд гурвалжны талууд болдог гэсэн учраас нэмэх утгуудтай байх ёстой гэдгээс 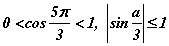 нөхцлүүд гарах бөгөөд Эндээс
нөхцлүүд гарах бөгөөд Эндээс 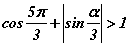 нөхцөл биелэхэд л хангалттай. Учир нь косинус, синусын утгууд нэгж радиустай тойрог дээр байгуулсан тэгш өнцөгтийн катетууд байдаг тул хоёр катетын нийлбэр гипотенуз буюу 1 -ээс их байхад л эдгээр нь гурвалжин үүсгэнэ. Иймээс a=1 гэж гарна.
нөхцөл биелэхэд л хангалттай. Учир нь косинус, синусын утгууд нэгж радиустай тойрог дээр байгуулсан тэгш өнцөгтийн катетууд байдаг тул хоёр катетын нийлбэр гипотенуз буюу 1 -ээс их байхад л эдгээр нь гурвалжин үүсгэнэ. Иймээс a=1 гэж гарна. - Гурвалжны нэг талыг хувиргавал
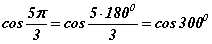 болох бөгөөд хувиргалтын томьёогоор
болох бөгөөд хувиргалтын томьёогоор 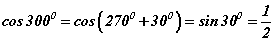 гэж гарах ба үүнийг
гэж гарах ба үүнийг 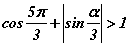 нөхцөлд тавиад модулийг задалбал
нөхцөлд тавиад модулийг задалбал 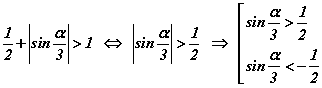 синусын утга 1/2 -ээс их эсхүл -1/2 -ээс бага байхад анхдагч тэнцэтгэл биш биелэнэ. Модулаас хэрхэн гаргахыг сайтын бусад бодлогоос үзээрэй. Эндээс b=1; c=1; гэж гарна.
синусын утга 1/2 -ээс их эсхүл -1/2 -ээс бага байхад анхдагч тэнцэтгэл биш биелэнэ. Модулаас хэрхэн гаргахыг сайтын бусад бодлогоос үзээрэй. Эндээс b=1; c=1; гэж гарна. - Сүүлд гаргасан тэнцэтгэл бишийг бодьё. Тригнометрийн тэнцэтгэл биш тэгшитгэлийг бодох үндсэн арга бол тэдгээрийг энгийн хэлбэрт оруулах байдаг. Иймээс α/3=t гэсэн орлуулга хийн энгийн тэнцэтгэл биш болгоод бодолтыг хийвэл
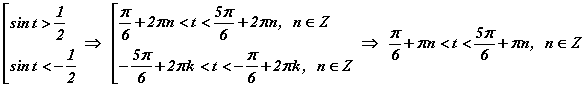 гэсэн хариу гарна. Бодолтыг нэгж тойрог дээр харуулбал
гэсэн хариу гарна. Бодолтыг нэгж тойрог дээр харуулбал 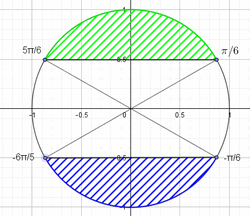 гэж харагдана. Зураг дээрх ногоон хэсэг бол синусын утга 0,5 -аас их байх хэсэг харин хөх хэсэг бол синусын утга -0,5 -аас бага байх хэсэг. Хэсгүүдийн хил хоорондох өнцгүүд тэнцэтгэл бишийг хангах бөгөөд синусын үеэр үелэх ёстой. Ер нь энгийн тэнцэтгэл биш, тэгшитгэлийн шийдийг цээжээр мэдэж байх ёстой. Үгүй бол асуудал үүснэ. Хоёр тэнцэтгэл бишийг тус тусд нь бодоод дараа нь шийдийг нэгтгэсэнг анхаарна уу. Синусын үе 2π байдаг ч шийдүүдийг нэгтгэхэд πn болно. Учир нь π/6 өнцөг -π гээр шилжихэд өөрөөр хэлбэл n=-1 үед -6π/5 утгыг авна. Шийдүүдийн хилүүд 180 буюу π -гээр шилжихэд хоёр тэнцэтгэл бишийг хангах утгын мужид шилжиж байгааг зурагт тэнхлэгийн эхийг дайран шийдүүдийн хилийг холбосон шугам тодорхой харуулна. Бодлогын тайлбар ойлгож байгаа хүнд илүү зүйл мэт боловч сайтын хэрэглэгчдийн мэдлэгийн түвшин өөр, сургалт талаасаа аль болохоор дэлгэрэнгүй тайлбарлахыг оролдсон болно. Бид α/3=t гэсэн орлуулга хийсэн учраас
гэж харагдана. Зураг дээрх ногоон хэсэг бол синусын утга 0,5 -аас их байх хэсэг харин хөх хэсэг бол синусын утга -0,5 -аас бага байх хэсэг. Хэсгүүдийн хил хоорондох өнцгүүд тэнцэтгэл бишийг хангах бөгөөд синусын үеэр үелэх ёстой. Ер нь энгийн тэнцэтгэл биш, тэгшитгэлийн шийдийг цээжээр мэдэж байх ёстой. Үгүй бол асуудал үүснэ. Хоёр тэнцэтгэл бишийг тус тусд нь бодоод дараа нь шийдийг нэгтгэсэнг анхаарна уу. Синусын үе 2π байдаг ч шийдүүдийг нэгтгэхэд πn болно. Учир нь π/6 өнцөг -π гээр шилжихэд өөрөөр хэлбэл n=-1 үед -6π/5 утгыг авна. Шийдүүдийн хилүүд 180 буюу π -гээр шилжихэд хоёр тэнцэтгэл бишийг хангах утгын мужид шилжиж байгааг зурагт тэнхлэгийн эхийг дайран шийдүүдийн хилийг холбосон шугам тодорхой харуулна. Бодлогын тайлбар ойлгож байгаа хүнд илүү зүйл мэт боловч сайтын хэрэглэгчдийн мэдлэгийн түвшин өөр, сургалт талаасаа аль болохоор дэлгэрэнгүй тайлбарлахыг оролдсон болно. Бид α/3=t гэсэн орлуулга хийсэн учраас 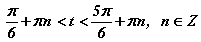 -ийг бодлогын шийд гэж ойлгож болохгүй. Орлуулгыг буцаан тавивал
-ийг бодлогын шийд гэж ойлгож болохгүй. Орлуулгыг буцаан тавивал 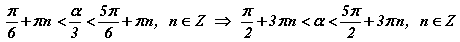 болох ба эндээс d=2; f=5; g=2; e=3 гэж гарна.
болох ба эндээс d=2; f=5; g=2; e=3 гэж гарна.
Хариу
a=1; b=1; c=1; d=2; f=5; g=2; e=3





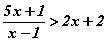 тэнцэл бишийг хангах x -ийн эерэг бүхэл утга хэд байх вэ?
тэнцэл бишийг хангах x -ийн эерэг бүхэл утга хэд байх вэ?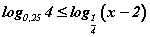 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.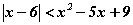 тэнцэл бишийг бод.
тэнцэл бишийг бод.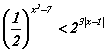 тэнцэтгэл бишийн шийд аль нь вэ?
тэнцэтгэл бишийн шийд аль нь вэ? илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.