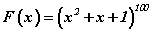 функцийн уламжлалыг ол.
функцийн уламжлалыг ол.
Жич: Энгийн мэт харагдах ч ээдрээтэй бодлого шүү. Уламжлалыг олж чадмаар байна уу.
Бодолт
Уламжлалыг олох функц нь нарийн төвөгтэй буюу давхар функц тул давхар функцыг дифференциалчлах 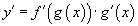 дүрмийг ашиглах хэрэгтэй. Давхар функцийн уламжлалыг олохдоо сурагчид муу байдаг нь ийм төрлийн бодлогууд ЭЕШ -д бага ирдэгтэй холбоотой байж болох ч үүнийг нарийн ойлгохгүйгээр математик анализийг ойлгох боломжгүй гэдгийг сануулъя. Давхар функцийг ойлгохын тулд a аргумент бүхий y(a)=a100 функцийг аваад үзье. Энэ бол a аргументтэй энгийн илтгэгч функц. Функц зөвхөн a аргументаас хамааралтай. Тэгвэл өгөгдсөн
дүрмийг ашиглах хэрэгтэй. Давхар функцийн уламжлалыг олохдоо сурагчид муу байдаг нь ийм төрлийн бодлогууд ЭЕШ -д бага ирдэгтэй холбоотой байж болох ч үүнийг нарийн ойлгохгүйгээр математик анализийг ойлгох боломжгүй гэдгийг сануулъя. Давхар функцийг ойлгохын тулд a аргумент бүхий y(a)=a100 функцийг аваад үзье. Энэ бол a аргументтэй энгийн илтгэгч функц. Функц зөвхөн a аргументаас хамааралтай. Тэгвэл өгөгдсөн 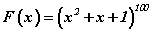 функцийг x -ээс хамаарсан илтгэгч функц гэж яагаад үзэж болохгүй гэж бодож байж болно. Функц нийтдээ x -ээс хамаарч байгаа хэдий ч илтгэгч функцийн аргумент x2+x+1 нь x -ээс хамааралтай бие даасан тусдаа функц гэдгээс
функцийг x -ээс хамаарсан илтгэгч функц гэж яагаад үзэж болохгүй гэж бодож байж болно. Функц нийтдээ x -ээс хамаарч байгаа хэдий ч илтгэгч функцийн аргумент x2+x+1 нь x -ээс хамааралтай бие даасан тусдаа функц гэдгээс 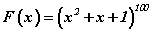 функцийг давхар функц гэж үзнэ. Хэрвээ y=x2+x+1 гэж үзвэл өгөгдсөн функцийг F(y)=y100 гэж үзэж болох бөгөөд энэ нь y(a)=a100 функцтэй ижил болж ирнэ. Эндээс
функцийг давхар функц гэж үзнэ. Хэрвээ y=x2+x+1 гэж үзвэл өгөгдсөн функцийг F(y)=y100 гэж үзэж болох бөгөөд энэ нь y(a)=a100 функцтэй ижил болж ирнэ. Эндээс 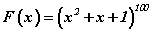 функцийг яагаад давхар гэж байгааг ойлгосон гэж бодож байна. Функцийн уламжлалыг
функцийг яагаад давхар гэж байгааг ойлгосон гэж бодож байна. Функцийн уламжлалыг 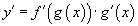 дүрмийг ашиглан тооцвол
дүрмийг ашиглан тооцвол 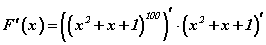 болно. Энд томьёоны
болно. Энд томьёоны 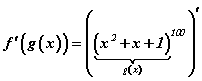 гэдгийг зөв ойлгох хэрэгтэй. Өөрөөр хэлбэл x2+x+1 аргументтэй функцийн уламжлалыг x2+x+1 аргументийн уламжлалаар үржүүлнэ гэсэн үг. Цааш хүснэгтийн уламжлалуудыг ашиглавал
гэдгийг зөв ойлгох хэрэгтэй. Өөрөөр хэлбэл x2+x+1 аргументтэй функцийн уламжлалыг x2+x+1 аргументийн уламжлалаар үржүүлнэ гэсэн үг. Цааш хүснэгтийн уламжлалуудыг ашиглавал 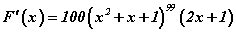 гэдгийг төвөггүй гаргана.
гэдгийг төвөггүй гаргана.
Хариу
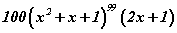





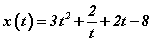 хуулиар хөдөлж байв. Хугацааны t=1 эгшинд ямар хурдтай байх вэ?
хуулиар хөдөлж байв. Хугацааны t=1 эгшинд ямар хурдтай байх вэ?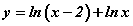 функцын өсөлт бууралтыг шинжил.
функцын өсөлт бууралтыг шинжил. тэгшитгэлийг бод.
тэгшитгэлийг бод.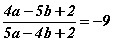 бол
бол 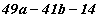 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.