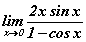 функцийн хязгаарыг ол.
функцийн хязгаарыг ол.
Бодолт
x -ийн оронд 0 -ийг тавивал 0/0 тодорхойгүй байдал үүсэхийг өөрсдөө шалгаарай. Тодорхойгүй байдал үүссэн тригнометрийн функцууд оролцсон илэрхийллийг ихэнхдээ нэгдүгээр гайхамшигт хязгаарын 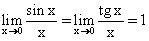 хэлбэрт оруулах гэж оролдох хэрэгтэй. Эхний ээлжинд хуваар дахь ялгаварыг хувирган үржвэр хэлбэрт оруулахын тулд косинус давхар өнцгийн
хэлбэрт оруулах гэж оролдох хэрэгтэй. Эхний ээлжинд хуваар дахь ялгаварыг хувирган үржвэр хэлбэрт оруулахын тулд косинус давхар өнцгийн 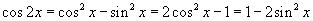 томьёог ашиглабал хязгаар
томьёог ашиглабал хязгаар 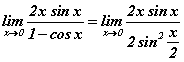 хэлбэрт шилжинэ. Ямар нэгэн үр дүн өгсөнгүй гэж яарах хэрэггүй. Бутархайн хүртвэрт синус давхар өнцгийн
хэлбэрт шилжинэ. Ямар нэгэн үр дүн өгсөнгүй гэж яарах хэрэггүй. Бутархайн хүртвэрт синус давхар өнцгийн 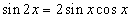 томьёог хэрэглэвэл
томьёог хэрэглэвэл 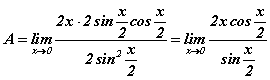 болно. x -ийн оронд 0 -ийг тавивал 0/0 тодорхойгүй байдал байсаар байна. Одоо яах вэ? Косинус функц тэг дээр нэг утгатай тул хуваарийг нэгдүгээр гайхамшигт хязгаарын хэлбэрт
болно. x -ийн оронд 0 -ийг тавивал 0/0 тодорхойгүй байдал байсаар байна. Одоо яах вэ? Косинус функц тэг дээр нэг утгатай тул хуваарийг нэгдүгээр гайхамшигт хязгаарын хэлбэрт 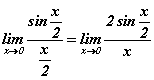 гэж оруулж болохоор байна. Тэгвэл хуваар, хүртвэрийг x/2 хуваавал
гэж оруулж болохоор байна. Тэгвэл хуваар, хүртвэрийг x/2 хуваавал 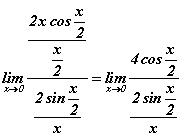 болно. Ногдворын хязгаар хүртвэр ба хуваарийн хязгааруудын ногдвортой тэнцүү дүрмээр хязгаарыг
болно. Ногдворын хязгаар хүртвэр ба хуваарийн хязгааруудын ногдвортой тэнцүү дүрмээр хязгаарыг 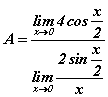 хэлбэрт оруулаад тооцоог хийвэл
хэлбэрт оруулаад тооцоог хийвэл 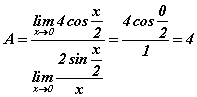 гарна. Хуваар нэгдүгээр гайхамшигт хязгаар буюу 1 тэнцүү гэдгийг санаарай.
гарна. Хуваар нэгдүгээр гайхамшигт хязгаар буюу 1 тэнцүү гэдгийг санаарай.
Зөвлөмж: Иймэрхүү бодлого ЭЕШ-д нилээд дээр ирж байсан ч сүүлийн жилүүдэд харагдахгүй болсон. ЭЕШ -д ирэхгүй болсон гэсэн утгаар ийм бодлогыг бодож сурах албагүй гэж бодвол маш том алдаа. Сүүлийн жилүүдийн шалгалтын материалууд маш хөнгөн болсон. ЭЕШ гэлтгүй ямар нэгэн шалгалтын материалыг дундаж хэмжээнд тохируулан зохиодог. Энэ нь таныг илүү нарийн бодлого бодохоос чөлөөлж байгаа хэрэг ердөө биш. Бодлого энгийн байсан ч тодорхой дүрэм, мэдлэг шаардана. Хэт энгийн томьёонд орлуулан тавих төрлийн бодлогууд дээр дадлага, бэлтгэл хийгээд том үр дүнг хүлээх хэрэггүй. Шалгалтад сайн, өндөр дүн авч байгаа хүмүүс яг ийм төрлийн бодлогыг бодон бэлтгэж байдаг учраас үүнээс энгийнийг тун төвөггүй шийдээд байгаа юм. Шалгалт тэмцээн хоёр нэг талаарай ижил зүйлүүд. Тамирчин хичнээн ачаалалтай сайн бэлтгэл хийнэ амжилт төчнөөн хэмжээнд дээшилдэгтэй л ижил шүү дээ.
Хариу
4





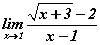 бод.
бод. үед
үед 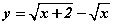 функцийн графикийн хэвтээ асимптотыг ол.
функцийн графикийн хэвтээ асимптотыг ол.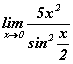 хязгаарыг бод.
хязгаарыг бод.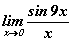 хязгаарыг ол.
хязгаарыг ол. тэгшитгэлийг бод.
тэгшитгэлийг бод.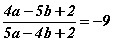 бол
бол 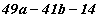 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.