Дарааллын эхний n гишүүний нийлбэр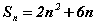 
томьёогоор өгөгджээ. Хэрэв энэ дараалал геометр прогресс бол q -г ол, арифметик прогресс бол d -г ол.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах
Бодлого 6.060
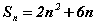Дараалал геометр прогресс бол q -г ол, арифметик прогресс бол d -г ол. (ЭЕШ 2017-A20)
Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.
Эхний гишүүн a1=3, ялгавар d=4 байх арифметик прогресс {an} ба a0=1 тооны хувьд
дараалал үүсгэвэл 
байна.- Үүссэн дарааллын
дугаар гишүүн 254 байна.
10 метрээс дээш гүнтэй худаг гаргуулахын тулд эхний нэг метрт 100 доллар дараагийн метр бүрд өмнөхөөсөө 50 доллар илүүг төлжээ. Үүнээс гадна бусад ажилд зориулан 1000 доллар нэмж төлсөн бөгөөд худгийн 1 метрийн дундаж өртөг 625 доллар болсон бол худгийн гүнийг тодорхойл.
Арифметик прогресс үүсгэдэг гурван тооны нийлбэр 2 харин эдгээр тоонуудын квадратуудын нийлбэр нь 14/9 бол нэг ба гуравдугаар тоонуудыг ол.
Нээгдсэн тоо : 1318
Энэ долоо хоногт
тэгшитгэлийг бод.
хязгаарыг бодоорой.