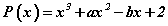 олон гишүүнт (x-1) олон гишүүнтэд үлдэгдэлгүй хуваагдах бөгөөд (x+2) ба (x-2) олон гишүүнтэд хуваахал ижил үлдэгдэл өгдөг бол a, b тоог олоорой.
олон гишүүнт (x-1) олон гишүүнтэд үлдэгдэлгүй хуваагдах бөгөөд (x+2) ба (x-2) олон гишүүнтэд хуваахал ижил үлдэгдэл өгдөг бол a, b тоог олоорой.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах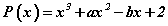 олон гишүүнт (x-1) олон гишүүнтэд үлдэгдэлгүй хуваагдах бөгөөд (x+2) ба (x-2) олон гишүүнтэд хуваахал ижил үлдэгдэл өгдөг бол a, b тоог олоорой.
олон гишүүнт (x-1) олон гишүүнтэд үлдэгдэлгүй хуваагдах бөгөөд (x+2) ба (x-2) олон гишүүнтэд хуваахал ижил үлдэгдэл өгдөг бол a, b тоог олоорой.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авахМэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.