m, n, p нь гурвалжны гурван талын урт бол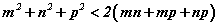 
гэдгийг батал
Бодолт
Ямарч гурвалжны хувьд хоёр талын уртын нийлбэр нь гуравдахь талынхаа уртаас их байдаг. Манай тохиолдолд m+n>p, n+p>m, m+p>n байна. Тэнцэл бишийг p-m<n, m-n<p, n-p<m гэж бичээд тэнцэл биш бүрийн хоёр талыг квадрат зэрэг дэвшүүлбэл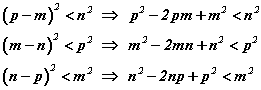 
болох бөгөөд эдгээр тэнцэл бишүүдийн хоёр талыг хооронд нь нэмбэл 
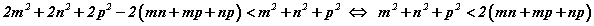болсноор батлах ёстой тэнцэл биш батлагдана.
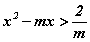тэнцэтгэл биш x -ийн дурын утганд биелэгдэх вэ?
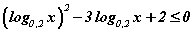тэнцэтгэл бишийн шийд аль вэ?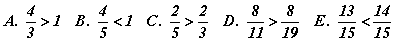
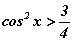тэнцэтгэл бишийн шийдийн олонлог аль вэ?
задаргааны хамгийн их нэмэгдхүүн 
бол a, b, c -г ол.
тэгшитгэлийг бод.
функцийн уламжлалын 
утгыг ол.