Хоёр шоог зэрэг орших туршилтын туссан нүднүүдийн нийлбэр ба давтамжаар дараах хүснэгтийг үүсгэе.
| Туссан нүдний тоо x | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Давтамж | 1 | 2 | 3 | 4 | 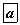 |
 |
5 |  |
3 | 2 | 1 |
P(x) -ээр x үзэгдлийн магадлалыг тэмдэглэвэл
Бодолт
Магадлалын бодлого бодоход та багахан хийсвэрлэж сэтгэх зайлшгүй хэрэгтэй. Хамгийн гол нь нийт үзэгдлийн тоо, ивээх үзэгдлийн тоог зөв тогтоовол магадлал олох амархан. Юуны өмнө бодлогын нөхцлийг зөв ойлгох. Бодлогын нөхцлийг харвал "Хоёр шоог зэрэг орших туршилт" гэж өгөгдсөн. Эндээс бидэнд хоёр шоо байгаад тэдгээрийг зэрэг буюу хамтад нь оршино гэсэн үг. Энгийн шоо 6 талтай, талууд 1-6 нүдтэй. Бодлогын нөхцөлд өөрөөр өгөөгүй болохоор шоо бол энгийн бидний мэдэх тоглоомд хэрэглэдэг шоо гэсэн үг. Шооны нүдний талаар жишээ нь хоёр тал нь гурван нүдтэй гэх мэт нөхцөл орж ирвэл бодлого хүндэрнэ. Гэхдээ ийм нөхцөлтэй бодлого ЕБС-ийн хэмжээнд бараг байдаггүй.
Нөхцөлд өгөгдсөн "туссан нүднүүдийн нийлбэр" гэдэг нь хоёр шоог оршиход хоёулаа аль нэг талаараа унаж таарна. Тэр унасан тал дээрх нүдний тооны нийлбэр гэж ойлгоно. Энэ нийлбэр бол 2-12 хооронд байж таарна. Учир нь шоо 1-6 нүдтэй тул хоёулаа 1-ээр буувал 2, хоёулаа 6 -аар буувал 12 гэсэн үг. Иймээс нүдний нийлбэр 2-12 завсраас гарахгүй. Нөхцөлд шоо булангаар буух талаар юу ч хэлээгүй болохоор туршилтад шоо заавал нэг талаараа бууна гэж тооцно. Хүснэгтийн нэгдүгээр мөрийн учрыг ойлгосон бол одоо 2-р мөрийн байхгүй тоог олоход амархан. Хоёр шоо хоёулаа 1 нүдээр бууж байж л буусан нүдний нийлбэр 2 болно. Өөрөөр нийлбэр 2 гарах боломжгүй тул давтамж нь 1 гэсэн үг. Өөрөөр хэлбэл ганцхан боломжтой буюу энэ үзэгдлийн ивээх үзэгдлийн тоо гэсэн үг.
Нийлбэр 3 байхын тулд нэг шоо 1-ээр нөгөө нь 2-оор буух ёстой. Хоёр шоо байгаа болохоор ийм үзэгдэл 2 байх учраас давтамж 2. Давтамжийг тоолж байгааг ойлгосон бол нийлбэр 6 байхын тулд {1; 5}, {2; 4}, {3; 3}, {4; 2}, {5; 1} гээд 5 боломжтой гэдгийг амархан тоолно. {1; 5} бичлэг эхний шоо 1 -ээр дараагийн шоо 5 -аар буухыг зааж байгаа болно. Эндээс a=5 болно. Ийм байдлаар тоовол b=6, c=4 гэдгийг амархан тогтооно. Ивээх үзэгдлийн тоонуудыг олсон. Одоо нийт үзэгдлийн тоог олъё. Шоо 6 -н талтай. Нэг шоо нэг талаараа буухад нөгөө шоо 6 -н янзаар буух боломжтой. Жишээ нь {1; 1}, {1; 2}, {1; 3}, {1; 4}, {1; 5}, {1; 6} цааш нэг шоо 2 нүдээр буухад бас 6 боломжтой. Эндээс нийт байж болох үзэгдлийн тоо 6·6=36 байна. Нийт үзэгдэл ивээх үзэгдлийн тоог мэдсэн болохоор магадлалыг олох томьёо хүснэгтээ ашиглан тооцоо хийх амархан. Ингээд
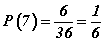 гэдгээс d=6 гэж гарна. P(7) -гэдэг нь буусан шоонуудын нүдний нийлбэр 7 байх магадлалыг ол гэсэн үг. Тэгэхлээр нийт үзэгдэл 36 харин нийлбэр 7 байх ивээх үзэгдэл 6 тул тоонуудыг томьёондоо тавивал 1/6 үр дүн гарна.
гэдгээс d=6 гэж гарна. P(7) -гэдэг нь буусан шоонуудын нүдний нийлбэр 7 байх магадлалыг ол гэсэн үг. Тэгэхлээр нийт үзэгдэл 36 харин нийлбэр 7 байх ивээх үзэгдэл 6 тул тоонуудыг томьёондоо тавивал 1/6 үр дүн гарна.- Энд 3≤x≤7 гэж өгсөн байгаа нь шоонуудын нийлбэр [3; 7] завсарт байх магадлалыг ол гэсэн үг. Үзэгдлүүд бие биенээсээ хамааралгүй учраас магадлал үзэгдлүүдийн магадлалын нийлбэртэй тэнцүү байна. Иймээс
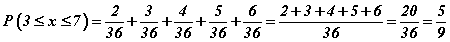 байх учраас e=5; f=9; болно.
байх учраас e=5; f=9; болно. - x≤6 бол 2-р магадлалтай ижилхэн тул
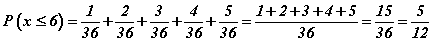 гээд g=5; h=2; байна.
гээд g=5; h=2; байна.
Жич: Эхлээд үзэгдлийн магадлалыг тооцоод дараа нь үр дүнгээс нөхөх тоо хэд байгааг олохыг анхаарна уу. Магадлалын бодлогыг бодох хичээлийг үзэхийг санал болгоё.
Хариу
a=5; b=6; c=4; d=6; e=5; f=9; g=5; h=2;





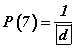
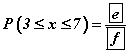
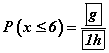
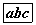 болно.
болно.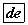 болно.
болно. тул олох магадлал
тул олох магадлал 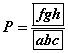 юм.
юм.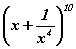 задрагааны x агуулаагүй гишүүнийг ол.
задрагааны x агуулаагүй гишүүнийг ол. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.