Материаллаг цэг шулуун шугамаар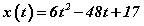 
хуулиар хөдлөнө. Энд x - хөдөлгөөний эхлэлийн цэгээс метрээр тооцсон зай. t - хөдөлгөөн эхлэснээс хойш секундээр тооцсон хугацаа бол t=9 секунд ашгинд дахь цэгийн хурдыг ол.
Бодолт
Уламжлалын талаар дурдаагүй байхад бодлогыг уламжлал хэсэгт оруулсанд гайхаж байна уу. Функц өгөгдөөд түүний уламжлалыг ол гэсэн байж л уламжлалын бодлого болохгүй. Уламжлал гэдэг ухагдхууны физик утга бол хурд байдаг. Тэгэхлээр ийм төрлийн бодлого шалгалт шүүлэгт орж ирвэл шууд л уламжлал ашиглах ёстойг ойлгоорой. Уламжлалын физик утгаар тодорхой цэг дээрх функцийн уламжлалын утга бол тухайн функцийн өөрчлөлтийн хурд байдаг. Иймээс бид эхлээд хөдөлгөөний хуулийн уламжлалыг олох хэрэгтэй. 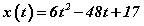функцийн уламжлалыг олохын тулд та нийлбэр , ялгаварыг дифференциалчлах
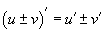дүрмээс гадна тогтмолыг дифференциалаас гаргах 
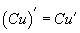, тогмолын уламжлалын 
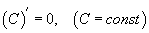, нэгдүгээр эрэмбийн үл мэдэгдэгчийн уламжлал 
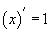, зэргийн уламжлалын 
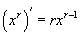томьёонуудыг мэдэж байх хэрэгтэй. 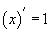томьёо бол 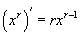томьёоны r=1 -ийн тухайн тохиолдол. Гэхдээ хэрэглэхэд амар үүднээс хоёр томьёог мэддэг байвал сайн. Функцийн уламжлалыг олцгооё. Энд би бүгдийг маш дэлгэрэнгүй тайлбарлая. Сайн ойлгоод аваарай.
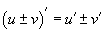- дүрмийн дагуу
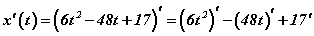байна. Илэрхийлэлд хичнээнч нийлбэр ялгавар байж болно. Дүрмийн дагуу илэрхийллийн гишүүн бүрийн уламжлал байдлаар задлаад бичнэ. Энд ямар нэгэн тэмдэг өөрчлөгдөх, хувиргалт байхгүй болохоор энгийн. - Одоо уламжлал бүр дээр тохирох дүрмийг хэрэглэнэ. Юуны өмнө тогтмолыг дифференциалаас гаргах 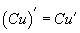, тогмолын уламжлалын 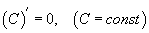дүрмийг хэрэглэвэл
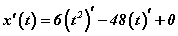болно. Томьёонуудыг ялган ойлгох хэрэгтэй. Сu гэдэг бол тогтмол тоог функцээр үржүүлсэн гэсэн үг. Энд манай 6t2, 48t гишүүд тохирно. t - ямар нэгэн утгыг авч болох учраас түүнийг функц гэж үзэж болно. Харин 17 бол жинхэнэ тогтмол. Өөрөөр хэлбэл ямар нэгэн өөрчлөлт байхгүй. Иймээс энд 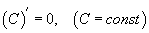томьёоны дагуу тэгийг тавина. - Эцэст нь 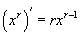томьёог хэрэглэвэл
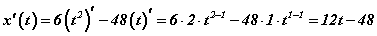гарна. Энэ бол хөдөлгөөний 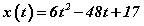хуулийн уламжлал. Хувьсагч ямар нэгэн зэрэггүй бол 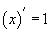байна. t -д нэг гэсэн зэрэг байгаа учраас 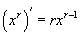томьёог хэрэглэж болно. x -ийн оронд sinx, cosx, logx, lnx гэх мэтээр өөрөө x -ээс хамаарсан функцууд байвал 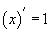үйлчлэхгүй. Жишээ нь 
, 
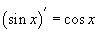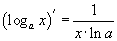гэх мэтээр өөр өөр байна. Ерөнхий тохиолдолд функцийн зэргийн 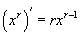томьёо бүгдэд нь үйлчилнэ. Өөрөөр хэлбэл sinx, cosx, logx, lnx гэх мэт функцууд зэрэгтэй байвал үйлчилнэ гэсэн үг
Уламжлал авах аргыг ойлгоод бодлогууд бодоод ирэхээр үйлдлүүдийг шууд цээжээр хийгээд сурдаг. Томьёонуудыг цээжлэх нэг хэрэг харин утгыг зөв ойлгохгүй бол ашиглах тал дээр хүндрэл гарах нь гарцаагүй. Хөдөлгөөний хуулийн уламжлалыг олсон болохоор t=9 секунд ашгинд дахь цэгийн хурд бол уламжлалын физик утгаар t=9 дээрх функцийн уламжлалын утгатай тэнцүү. Эндээс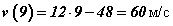 
байна.
Хариу
60 м/с
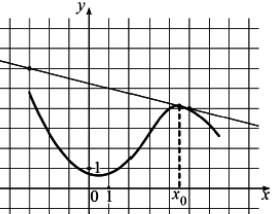Зурагт y=f(x) функцийн график ба түүнийг x0 абциссттай цэгт шүргэсэн шүргэгчийг үзүүлжээ. y=f(x) функцийн x0 цэг дээрх уламжлалын утгыг ол.
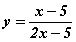функцийн уламжлалын x=3 цэг дээрх утгыг ол.
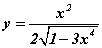функцийн уламжлалыг ол.
задаргааны хамгийн их нэмэгдхүүн 
бол a, b, c -г ол.
тэгшитгэлийг бод.
функцийн уламжлалын 
утгыг ол.