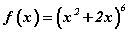бол 
олон гишүүнтийн x5 -ийн өмнөх коэффициентийг ол.
Бодолт
Өгөгдсөн олон гишүүнтийн уламжлалыг тооцоё. 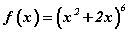бол давхар функц. Энэ дээр сурагчид их төөрдөг. Хэрвээ f(x)=x6 гэж байсан бол дан функц болно. Учир нь функц ганцхан x -ээс хамааралтай байгаа. 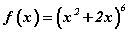функц ч бас л ганц x -ээс хамааралтай байгаа мэт санагдаж магадгүй. Тэгвэл 
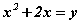гэж үзвэл функц 
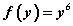хэлбэрт шилжээд дан функц болно. Гэтэл y функц өөрөө x -ээс хамааралтай байгаа тул давхар функцийн уламжлалын 
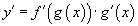томьёогоор тооцно. Өгөгдсөн функцийн хувьд 
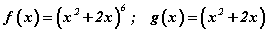гэсэн үг. Эндээс томьёоны дагуу 
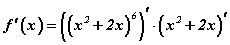байна. Одоо уламжлалын 
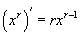томьёог ашиглан тооцвол 
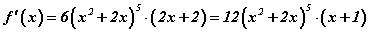гэж гарна. Хоёрдахь хаалтыг задалбал өгөгдсөн функцийн уламжлал 
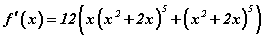болно.
Одоо олон гишүүнтийн задаргааны x5 -ийн өмнөх коэффициентийг олох хэрэгтэй. Хаалтанд хоёр задаргаа байгаа эхний задаргаа x -ээр үржигдэнэ гэдгээс эхний задаргааны x4 -ийн харин хоёрдахь задаргааны x5 -ийн өмнөх коэффициентүүдийн нийлбэрийг 12 -оор үржүүлэхэд олох ёстой хариу гарна. Нийлбэрт байгаа олон гишүүнт ижилхэн учраас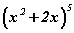 
олон гишүүнтээс Ньютоны биномыг 
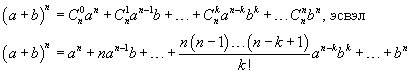ашиглан коэффициентүүдийг тооцоё. Томьёоны дагуу задаргаа 
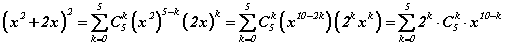байх ёстой. Нийлбэр дотор x4 гишүүн 
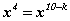тэгшитгэлийг хангах k -гийн утганд гарах ёстой. Тэгшитгэлийг бодвол 4=10-k гэдгээс k=6 гэж гарна. k>5 учраас задаргаанд x4 гишүүн үүсэхгүй. Харин 
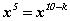тэгшитгэлээс k=5 гэж гарах тул задаргаанд 
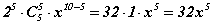гишүүн байгаа. Эндээс задаргаанд x4 -тэй гишүүн байхгүй тул эхний нэмэгдхүүнээс x5 -тэй гишүүн гарахгүй /нэмэгдхүүнийг x -ээр үржиж байгаа/ харин хоёрдахь нэмэгдхүүнд 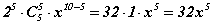гишүүн байгаа. Эндээс x5 -ийн өмнөх коэффициент 12·32=384 гэж гарна.
Санамж: Бодлогод нилээд хугацаа зарцуулах хэрэг гарч мэднэ. Иймээс эхний удаад бодлоготой ноцолдох хэрэггүй шууд өнгөрөөгөөд амархан бодлогуудаа шийдсний дараа барьж авах хэрэгтэй. Давхар функцийн уламжлал, Ньютоны биномыг сайн ойлгосон бол асуудалгүй шийднэ. Хэрвээ эдгээрийг мэдэхгүй бол бодохгүй гэсэн үг.
Жич: Бодлогыг бодож дийлэхгүй бол санаа зоволтгүй. Заавал бүгдийг бодох албатай биш. Эцсийн арга бол таах. Таахдаа шууд бингодох хэрэггүй. 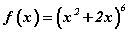функцийн уламжлал задаргаанд ямарч сөрөг тэмдэг гарч ирэхгүй нь тодорхой. Иймээс сөрөг тэмдэгтэй B, E хариунууд тохирохгүй. Хэрвээ уламжлалыг олж чадсан бол цааш бодолгүй таачих боломжтой. Нэг тоог 12 -оор үржүүлэх хариу гарах болж таарна. D хариу 12 -д тэгш хуваагдахгүй учраас биш. Харин A, C хариунууд 768/12=64, 384/12=32 гэж тэгш хуваагдана. Уламжлалын зэрэг 5 харин задаргааны хоёрдахь гишүүний 2 коэффициентийн 5 зэрэг 32 гэдгээс С хариуг таан сонгож болно.
Хариу
384
-ийн x4 -ийн коэффициентийг ол.
тэнцэтгэл бишийн шийд 
тэнцэтгэл бишийн шийд болох магадлал 
байна.
илэрхийллийг хялбарчил
ABCD трапецийн бага диагонал BD=6 бөгөөд суурьтай перпендикуляр. Трапецийн AD=3, DC=12 бол B, D мохоо өнцгийн нийлбэрийг ол.