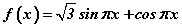 функц өгөгджээ.
функц өгөгджээ.
I. 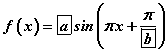 хэлбэрт оруулсан.
хэлбэрт оруулсан.
II. Үндсэн үе нь  байна.
байна.
III. 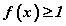 тэнцэтгэл бишийн шийд нь
тэнцэтгэл бишийн шийд нь 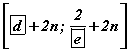 байна. Энд
байна. Энд 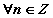 байна.
байна.
IV. f(x) функцийн x0=1 абцисстай M цэгт татсан шүргэгч шулууны тэгшитгэл 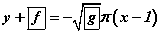 байна.
байна.
Бодолт
I. Даалгаварыг биелүүлэх түлхүүр бол өнцгүүдийг нийлбэрийн синусыг задлах 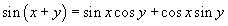 томьёо юм. Томьёог ашиглаад өгөгдсөн
томьёо юм. Томьёог ашиглаад өгөгдсөн 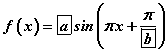 хариуд хувиргалт хийвэл
хариуд хувиргалт хийвэл 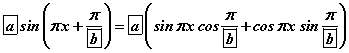 болно. Хаалтыг задлахад өгөгдсөн функц гарч ирж байхын тулд
болно. Хаалтыг задлахад өгөгдсөн функц гарч ирж байхын тулд 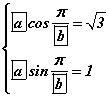 системийг хангах a, b гийн утгуудыг олох хэрэгтэй. Хоёрдугаар тэгшитгэлийг нэгдүгээр тэгшитгэлд хуваавал
системийг хангах a, b гийн утгуудыг олох хэрэгтэй. Хоёрдугаар тэгшитгэлийг нэгдүгээр тэгшитгэлд хуваавал 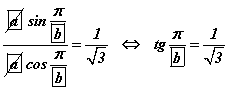 гэж гарах бөгөөд тэгшитгэлийн шийд
гэж гарах бөгөөд тэгшитгэлийн шийд 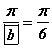 байна. Одоо утгыг системийн 2 -р тэгшитгэлд орлуулан бодвол
байна. Одоо утгыг системийн 2 -р тэгшитгэлд орлуулан бодвол 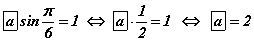 гэж гарна. Өгөгдсөн функцийг
гэж гарна. Өгөгдсөн функцийг 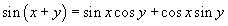 томёёогоор хувиргавал
томёёогоор хувиргавал 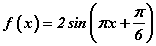 хэлбэрт орно гэдгээс a=2; b=6; байна.
хэлбэрт орно гэдгээс a=2; b=6; байна.
II. Тригнометрийн функцийн үеийг олох 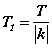 томьёо байдаг. Үүнийг цээжлээд аваарай. Энд Т бол y=f(x) функцийн үе, k нь үл мэдэгдэгчийн коэффициент юм. Манай тохиолдолд эхний даалгавараас өгөгдсөн функц
томьёо байдаг. Үүнийг цээжлээд аваарай. Энд Т бол y=f(x) функцийн үе, k нь үл мэдэгдэгчийн коэффициент юм. Манай тохиолдолд эхний даалгавараас өгөгдсөн функц 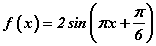 хэлбэрт шилжсэн байгаа. Синус функцийн үе 2π байдаг x -ийн коэффициент π гэдгийг томьёонд тавибал
хэлбэрт шилжсэн байгаа. Синус функцийн үе 2π байдаг x -ийн коэффициент π гэдгийг томьёонд тавибал 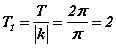 болох ба c=2; гэж гарна.
болох ба c=2; гэж гарна.
III. Даалгавар бол 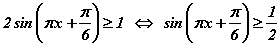 тэнцэтгэл бишийг бодох юм. sinx≥a тэнцэтгэл бишийн шийд
тэнцэтгэл бишийг бодох юм. sinx≥a тэнцэтгэл бишийн шийд 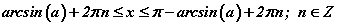 байдаг гэдгээс
байдаг гэдгээс 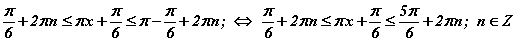 гэж гарна. Бүх талаас π/6 -г хасвал
гэж гарна. Бүх талаас π/6 -г хасвал 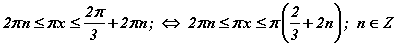 гарах бөгөөд бүгдийг π -д хуваавал
гарах бөгөөд бүгдийг π -д хуваавал 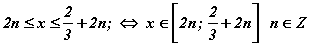 гэж гарснаар d=0; e=3; болно.
гэж гарснаар d=0; e=3; болно.
IV. Даалгаварыг гүйцэтгэхийн тулд та y=f(x) функцын графикт x=a цэгт шүргэгчийн тэгшитгэлийн 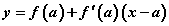 томьёог мэддэг байх хэрэгтэй. Эхлээд x0=1 абцисстай цэгт функц ямар утгатай байхыг олвол
томьёог мэддэг байх хэрэгтэй. Эхлээд x0=1 абцисстай цэгт функц ямар утгатай байхыг олвол 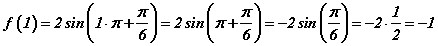 гэж гарна. Энд
гэж гарна. Энд 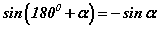 хувиргалтын томьёог мэдэж байх ёстой шүү. Функцийн уламжлалыг тооцохдоо давхар функцыг дифференциалчлах
хувиргалтын томьёог мэдэж байх ёстой шүү. Функцийн уламжлалыг тооцохдоо давхар функцыг дифференциалчлах 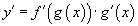 дүрмээр
дүрмээр 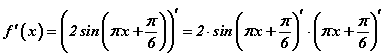 гэж үзээд функц бүрийн уламжлалыг
гэж үзээд функц бүрийн уламжлалыг 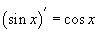 ,
, 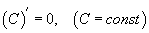 ,
, 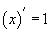 томьёонуудыг ашиглан тооцвол
томьёонуудыг ашиглан тооцвол 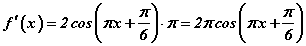 гэж гарна. Шүргэгчийн тэгшитгэлийн дагуу x0=1 абцисстай цэг дээрх уламжлалын утгыг олвол
гэж гарна. Шүргэгчийн тэгшитгэлийн дагуу x0=1 абцисстай цэг дээрх уламжлалын утгыг олвол 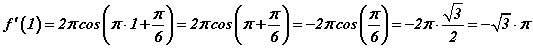 гэж гарна. Олсон утгуудыг
гэж гарна. Олсон утгуудыг 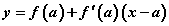 томьёонд тавиад өгөгдсөн утгын хэлбэрт шилжүүлбэл
томьёонд тавиад өгөгдсөн утгын хэлбэрт шилжүүлбэл 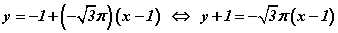 гэж гарна. Эндээс f=1; g=3; гэж гарна.
гэж гарна. Эндээс f=1; g=3; гэж гарна.
Жич: Элсэлтийн шалгалтын 2-р хэсгийн бодлогууд нилээд хугацаа авах олон сэдвийг хамарсан байдаг тул тэдгээрт хугацаа гаргахын тулд эхний хэсгийг маш хурдан зөв бодоод хариуны хуудсаа бөглөөд дараа нь 2-р хэсэгт шилжих нь дээр. Тэгэхгүй бол 2-р хэсэгт цаг алдсанаас болоод хариуны хуудсаа бөглөх цаггүй болох эрсдэлтэй.
Хариу
a=2; b=6; c=2; d=0; e=3; f=1; g=3;





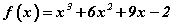 функц [-2; 5] завсрын аль хэсэгт буурах вэ?
функц [-2; 5] завсрын аль хэсэгт буурах вэ?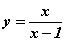 функц өгөгдөв.
функц өгөгдөв.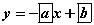
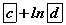
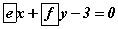
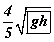
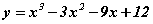 функцийн буурах завсрыг ол.
функцийн буурах завсрыг ол. задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.