Евклид геометрийн аксиомууд

Хавгайн геометрт ихэнхдээ ашиглагддаг аксиомуудыг авч үзье

  1. Харьяаллын аксиом. Хавтгай дээрх дурын хоёр цэгийг дайруулж цорын ганц  шулуун татна.
  2. Дарааллын аксиом. Шулуун дээрх гурван цэгээс хоёр цэгийнхээ дунд орших нэг цэг олдоно.
  3. Хэрчим өнцөгийн тэнцлийн аксиом. Хэрвээ хоёр өнцөг юмуу хэрчим гуравдагч өнцөг юмуу хэрчимтэй тэнцүү бол тэдгээр нь өөр хоорондоо тэнцүү байна.
  4. Паралель шулууны аксиом. Шулууны гадна орших дурын нэг цэгийг дайруулан уг шулуунтай паралель цорын ганц шулуун татаж болно.
  5. Үргэлжлэлийн аксиом. / Архимедын аксиом /  AB ба CD дурын хоёр хэрчмийн хувьд 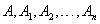гэсэн төгсгөлөг цэгийн багц байна. Тэгвэл AB хэрчим дээр байгаа 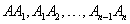хэрчмүүд нь CD дээрх хэрчмүүдтэй тэнцүү бөгөөд A ба 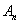хооронд B цэг оршино.

Эдгээр аксиомуудыг өөр байдлаар хэрэглэвэл батлах хэрэгтэй теорем болж хувирахыг тэмдэглэе. Жишээлбэл гурвалжны өнцгийн шинжийн аксиомд паралель шулууны аксиомыг чанар болгон ашиглавал паралель шулууны аксиомыг батлах хэрэгтэй болно.

Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.

Холбоотой материалууд
Тригнометрийн тэнцэл биш

  Нээгдсэн тоо: 2581 Нийтийн

Тригнометрийн тэнцэл бишийг бодохдоо алгебрын тэнцэл бишийн шинжүүд болон төрөл бүрийн тригнометрийн хувиргалт, томьёонуудыг ашиглана. Тригнометрийн тэнцэл бишийг бодоход нэгж тойрогийг ашиглах нь бараг гарцаагүй байдаг.

Жишээ 1
тэнцэл бишийг бод.

Бодолт
Нэгж тойргийн радиусын нэг эргэлтэд энэ тэнцэл биш нь 0 < x < π үнэн байна. Одоо синусын үе 2πn ийг нэмэх шаардлагатай. : 

Гурвалжны периметр, талбай

  Нээгдсэн тоо: 20083 Нийтийн

Хаалттай тахир шугаман дүрсүүд периметр, талбайтай байдаг. Гурвалжин ч хаалттай тахир шугамаар үүсдэг дүрс тул хичээлээр гурвалжны периметр, талбайн талаар авч үзье.

Жич: Геометрийн бодлогод периметр, талбайг ол гэсэн нөхцөл байхаас тухайн ухагдхуун гэж юу болох хэрхэн тооцохыг та өөрөө мэдэж байхыг шаардана. Ухагдхууныг мэдэхгүй, яаж тооцохыг мэдэхгүй бол бодлогыг бодохгүй л гэсэн үг.

Хавтгай дүрсүүдийн талбай

  Нээгдсэн тоо: 4763 Бүртгүүлэх

Энэ хэсэгт бид хавтгай дүрсийн талбайг олоход өргөн хэрэглэдэг томьёонуудыг авч үзнэ.
Квадрат /Зур. 58/ a - тал , d - диагнал.

Тэгш өнцөгт /Зур. 59/ a, b - талууд.

Биетийн төстэй шинж

  Нээгдсэн тоо: 2188 Нийтийн

Нэг нь нөгөөгийнхөө бүх шугаман хэмжээсийг нэг ижил харьцаагаар исэхгэх юмуу багасгах замаар гаргасан хоёр биетийг төстэй биет гэнэ. Автомашин түүний модел хоёр нь төстэй биетүүд.

Биетийн төстэй байх шинжүүд:

  • Хоёр цилиндр эсвэл конусын сууриудын радиус нь өндөртэйгээ порпорционал байвал төстэй байна
  • Хоёр ба түүнээс дээш биетүүдийн хавтгай болон муруй гадаргуунуудын талбайнууд нь дурын харгалзах хэрчмийн квадратад порпорционал байвал тэдгээр нь төстэй байна.
  • Хоёр ба түүнээс дээш биетүүдийн эзэлхүүнүүд нь дурын харгалзах хэрчмийн кубэд порпорционал байвал тэдгээр нь төстэй байна.
Статик гишүүд…

Класс ба структурт ердийн талбар, арга, шинжүүдээс гадна статик талбар, арга, шинжүүд байж болдог. Статик талбар, арга, шинжүүд…

Нээгдсэн тоо : 44

 
useRef

Хичээлээр useState -тэй тун төстэй useRef хукийн талаар авч үзье. useRef хукийн онцлог ашиглалтыг компонент хэдэн удаа дахин…

Нээгдсэн тоо : 43

 
Тоог ихэсгэх

Хүүхдүүд тооны хичээлийг анхнаасаа зөв ойлгон сураагүйгээс анги ахих тусмаа математикийн хичээлийнн хоцрогдолоос болоод дургүй болох тал байдаг.…

Нээгдсэн тоо : 103

 
Графикийн паттерн.…

Нийтлэлээр графикийн хэвүүдийн /GUI pattern/ түүхийг авч үзье. Боловсруулалтын графикийн хэвүүдийг 30 гаруй жилийн туршид боловсруулж байгаа бөгөөд…

Нээгдсэн тоо : 82

 
Аргын хэт…

Хааяа өөр өөр параметрүүдийн багцтай нэг аргыг үүсгэх шаардлага гардаг. Ирсэн параметрүүдээс хамааран аргын тодорхой хэрэгжүүлэлтийг хэрэглэнэ. Ийм…

Нээгдсэн тоо : 80

 
Vuex -ийг…

Ямарч програмын ажиллагааны чухал хэсэг бол төрөл бүрийн мэдээллийн боловсруулалт, тэдгээртэй ажиллахтай холбоотой байдаг. Иймээс энэ хичээлээс vuejs…

Нээгдсэн тоо : 65

 
useEffect

Хичээлээр react -ийн хукуудаас их өргөн ашиглагддаг useEffect -ийн талаар авч үзье. useEffect -ийн ажиллагааг судлах хуудасны кодийг

…

Нээгдсэн тоо : 61

 
Тоон болон…

Илэрхийлэл бол математикийн хэлний үндэс болсон суурь ойлголтуудын нэг. Математикийн илэрхийллийг тооцооны алгоритм, аксиом, теорем, бодлогын нөхцлүүд гээд…

Нээгдсэн тоо : 78

 
Програмчлалын хэвүүд…

Програм зохиох бол нарийн төвөгтэй ажил. Ямар ч програмын хувьд өөрийн хийх ажлаа гүйцэтгэхийн чацуу цаашдаа хөгжих, ажлын…

Нээгдсэн тоо : 74

 
© 2014 Зохиогчийн эрхээр хамгаалагдсан. Холбогдох