P оройтой суурийн тал нь 3, өндөр нь 2 зөв тэгш өнцөгт PABCD пирамидын A оройгоос PCD таслт хүртлэх зайг ол.
Бодолт
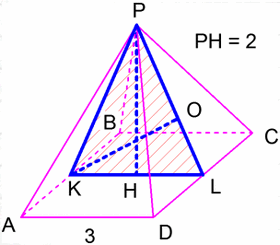DC хэрчим PDC хавтгайд харьяалагдана. Харин AB энэ хавтгайд оршихгүй ч DC -тэй паралел. Эндээс AB хэрчим PDC хавтгайтай паралел байна. Иймээс AB -гийн дундаж K цэгээс PDC хавтгай хүртлэх зай бол олох ёстой A оройгоос PCD таслт хүртлэх зайтай тэнцүү гэдэг нь батлагдана.
Пирамид зөв учраас H цэг ABCD суурийн төвд байрлана. Өөрөөр хэлбэл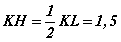 
гэсэн үг. PLH тэгш өнцөгт гурвалжнаас 
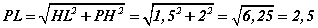байна. PKL гурвалжны талбай нэг талаас 
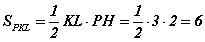харин нөгөө талаас 
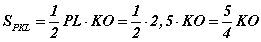гэдгээс 
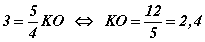байна.
Хариу
2,4
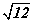бол түүний ирмэгийн уртын нийлбэрийг ол.
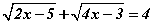тэгшитгэл бод.
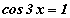тэгшитгэл бод.
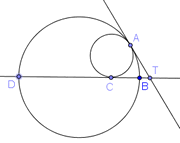Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.