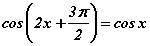 тэгшитгэлийг бод.
тэгшитгэлийг бод.
Жич: Нэг аргаар олон бодлого бодсноос нэг бодлогыг олон аргаар шийд.
Бодолт
Нэг аргаар олон бодлого бодсноос нэг бодлогыг олон аргаар шийдэх илүү өгөөжтэй тул энэ бодлогын 3 шийдлийг авч үзье.
1-р арга.
Тэгшитгэлийн зүүн талыг хувиргалтын эсхүл нийлбэрийн косинусийн 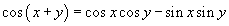 томьёог хэрэглэн хувиргавал
томьёог хэрэглэн хувиргавал 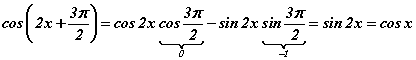 тэгшитгэлд шилжинэ. Цааш синус давхар өнцгийн
тэгшитгэлд шилжинэ. Цааш синус давхар өнцгийн 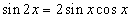 томьёог ашиглан хувиргавал
томьёог ашиглан хувиргавал 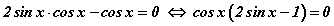 тэгшитгэл үүснэ. Үржвэр тэгтэй тэнцэх нөхцлөөр
тэгшитгэл үүснэ. Үржвэр тэгтэй тэнцэх нөхцлөөр 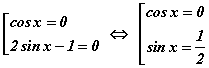 энгийн тэгшитгэлүүдийн багц үүснэ. Эндээс
энгийн тэгшитгэлүүдийн багц үүснэ. Эндээс 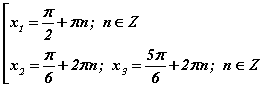 гэсэн шийдийн багц гарна. Тригнометрийн энгийн тэгшитгэлүүдийн шийдийг цээжээр мэдэж байх хэрэгтэйг зөвлөе.
гэсэн шийдийн багц гарна. Тригнометрийн энгийн тэгшитгэлүүдийн шийдийг цээжээр мэдэж байх хэрэгтэйг зөвлөе.
2-р арга.
Анхдагч тэгшитгэлийн баруун хэсгийг тэнцүүгийн тэмдгийн зүүн талд гаргавал 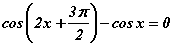 болно. Одоо косинус функцуудийн ялгаварын
болно. Одоо косинус функцуудийн ялгаварын 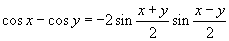 томьёогоор
томьёогоор 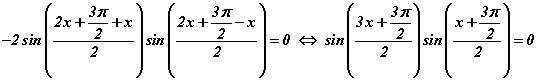 тэгшитгэл үүснэ. Үржвэр тэгтэй тэнцэх нөхцлөөр
тэгшитгэл үүснэ. Үржвэр тэгтэй тэнцэх нөхцлөөр 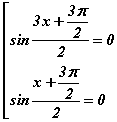 тэгшитгэлийн багц үүснэ. sinx=0 тэгшитгэлийн шийд x=πn гэдгээс
тэгшитгэлийн багц үүснэ. sinx=0 тэгшитгэлийн шийд x=πn гэдгээс 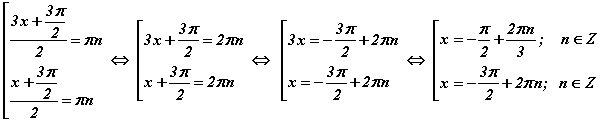 шийдүүд гарч ирнэ. Шийд эхний шийдтэй тэнцүү биш гэж харж байна уу. 2-р аргын шийдийг
шийдүүд гарч ирнэ. Шийд эхний шийдтэй тэнцүү биш гэж харж байна уу. 2-р аргын шийдийг 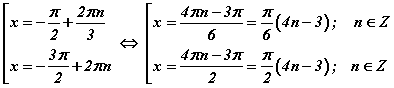 хэлбэрт оруулбал Эхний бүлэг шийдээс
хэлбэрт оруулбал Эхний бүлэг шийдээс 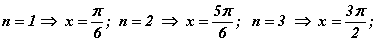 цэгүүд гарч ирэх бөгөөд цааш n-ийн утгуудад 1-р аргын хоёрдахь бүлгийн шийдүүд давтагдана. Харин хоёрдахь бүлэг шийдээс
цэгүүд гарч ирэх бөгөөд цааш n-ийн утгуудад 1-р аргын хоёрдахь бүлгийн шийдүүд давтагдана. Харин хоёрдахь бүлэг шийдээс 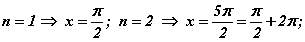 гээд цааш 1-р аргын нэгдүгээр бүлгийн шийдүүд давтагдана.
гээд цааш 1-р аргын нэгдүгээр бүлгийн шийдүүд давтагдана.
Жич: Шалгалтаар 1 ба 2 -р аргын шийдүүд ижил гэдгийг тогтоох нь тригнометрийн функцийн үелэх чанарыг ойлгох, тэгшитгэлийн шийдийг тодорхойлоход сайн дадлага болохыг сануулъя.
3-р арга.
Өгөгдсөн тэгшитгэлийг зэрэгт эсхүл логарифм тэгшитгэлүүд шиг аргументууд нь 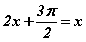 тэнцүү бол функцуудын утгууд тэнцэнэ гэж үзэж болно. Энэ зөв үү. Яг зөв гэхэд хэцүү. Жишээ нь 60<>420 хэдий ч cos600=cos4200 нь 1/2=1/2 утгуудаар тэнцэнэ. Тригнометрийн функцийн үеийг харгалзан үүнийг
тэнцүү бол функцуудын утгууд тэнцэнэ гэж үзэж болно. Энэ зөв үү. Яг зөв гэхэд хэцүү. Жишээ нь 60<>420 хэдий ч cos600=cos4200 нь 1/2=1/2 утгуудаар тэнцэнэ. Тригнометрийн функцийн үеийг харгалзан үүнийг 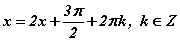 гэж засая. Энд ч бас асуудал бий. Косинус тэгш функц учраас cos600=cos(-600) нь 1/2=1/2 байна. Тэгвэл үүнийг тусган өгвөл функцуудийн аргументууд
гэж засая. Энд ч бас асуудал бий. Косинус тэгш функц учраас cos600=cos(-600) нь 1/2=1/2 байна. Тэгвэл үүнийг тусган өгвөл функцуудийн аргументууд 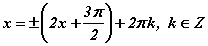 тэнцлийг хангах x -ийг тэгшитгэлийн шийд гэж үзэж болно. Эндээс
тэнцлийг хангах x -ийг тэгшитгэлийн шийд гэж үзэж болно. Эндээс 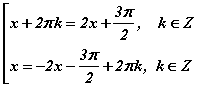 гэсэн хоёр тохиолдолд гарч ирнэ. Өөрөөр хэлбэл баруун функцийн аргумент тодорхой үеэр зүүн функцийн аргументтэй тэнцэх эсхүл зүүн функцийн сөрөг утга тодорхой үеэр баруун функцийн аргументтэй тэнцүү байна гэсэн үг. Эндээс
гэсэн хоёр тохиолдолд гарч ирнэ. Өөрөөр хэлбэл баруун функцийн аргумент тодорхой үеэр зүүн функцийн аргументтэй тэнцэх эсхүл зүүн функцийн сөрөг утга тодорхой үеэр баруун функцийн аргументтэй тэнцүү байна гэсэн үг. Эндээс 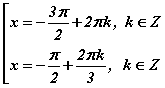 гэсэн 2-р аргынхтай ижил шийдүүд гарч ирнэ.
гэсэн 2-р аргынхтай ижил шийдүүд гарч ирнэ.
Хариу
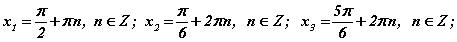





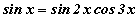 тэгшитгэлийг бод.
тэгшитгэлийг бод.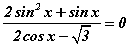 тэгшитгэл
тэгшитгэл 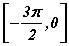 завсарт хэдэн шийдтэй вэ?
завсарт хэдэн шийдтэй вэ?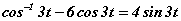 тэгшитгэлийг бод.
тэгшитгэлийг бод.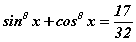 тэгшитгэлийг бод.
тэгшитгэлийг бод.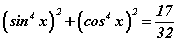 гэдгээс ялгаврын бүтэн квадрат бичвэл
гэдгээс ялгаврын бүтэн квадрат бичвэл 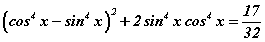 болох ба
болох ба 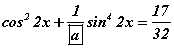 болно.
болно.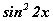 -ийн хувьд
-ийн хувьд 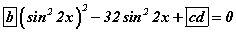 квадрат тэгшитгэлд шилжих учир боломжит шийд нь
квадрат тэгшитгэлд шилжих учир боломжит шийд нь 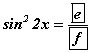 .
. 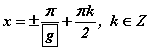 болно.
болно.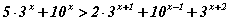 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.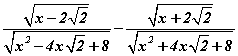 илэрхийллийн x=3 утгыг ол.
илэрхийллийн x=3 утгыг ол.