Зургаан оронтой тоо 2 цифрээр эхэлдэг. Хэрвээ түүнийг эхний байрлалаас сүүлийн байрлалд шилжүүлэхдээ бусад цифрүүдийн байрлалыг хадгалвал анхдагч тооноос гурав дахин их тоо үүсэх бол анхдагч тооны цифрүүдийн нийлбэрийг ол.
Бодолт
Анхдагч зургаан оронтой тооны эхний 2 цифрийн ардах таван оронтой тоог x гэе. Тэгвэл анхдагч тооны аравтын хэлбэр (2·105+x) харин шинээр үүсэх тооны аравтын илэрхийлэл (10x+2) байна. Энд натурал тооны аравтын хэлбэрийн бичлэгийг ойлгох хэрэгтэй. a0a1a2a3...an-1an хэлбэрийн n+1 оронтой натурал тоо байлаа гэе. Энд an нэгжийн an-1 аравтын an-2 зуутын орон гээд явна. Тэгвэл a0a1a2a3...an-1an хэлбэрийн натурал тоог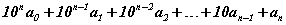 
гэж аравтын хэлбэрээр илэрхийлж болдогийг мэдэх хэрэгтэй. Жишээ нь 327=3·102+2·10+7, 5248=5·103+2·102+4·10+8 гэх мэтээр. Эндээс л дээрх (2·105+x) ба (10x+2) хоёр илэрхийлэл гарч ирж байгаа хэрэг. Анхдагч тоо зургаан оронтой бөгөөд эхний цифр нь 2 тул түүнийг 105 үржүүлээд ардах таван оронтой тоог x -ийг нэмвэл (2·105+x) буюу анхдагч тоотой тэнцүү. Эхний цифрийг сүүлийн байрлалд шилжүүлэхдээ бусад цифрүүдийг байрлалыг хадгалсан тул үүсэх тоог аравтын хэлбэрээр (10x+2) гэж бичиж болохыг ойлгосон гэж үзье.
Санамж: Сайн ойлгохгүй байвал ямар нэгэн 6 оронтой тоо аваал туршаад үзээрэй.
Цааш бодлогын нөхцлөөр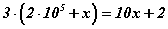 
тэгшитгэл үүсэх бөгөөд 
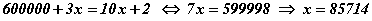гэж гарна. Эндээс анхдагч тоо 285714 болох бөгөөд цифрүүдийн нийлбэр нь 27 гарна.
Жич: Анхдагч тоог олох даалгавар өгөгдөн сонгох тест байвал хариунаас нь хөөн бодох боломж гардаг тул цифрүүдийн нийлбэрийг олох нэмэлт оруулсан хэрэг.
Хариу
27
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.