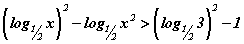 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.
Бодолт
Тэнцэтгэл бишийн тодорхойлогдох муж 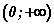 гэдгийг тооцон зэргийн логарифмийн
гэдгийг тооцон зэргийн логарифмийн 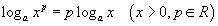 томьёог ашиглан тэнцэтгэл бишийг
томьёог ашиглан тэнцэтгэл бишийг 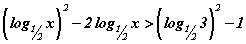 хэлбэрт оруулая.
хэлбэрт оруулая. 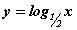 гэж үзвэл
гэж үзвэл 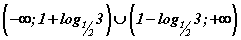 шийдийн олонлогтой
шийдийн олонлогтой 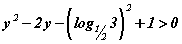 тэнцэтгэл биш үүснэ. Тэнцэтгэл бишийн шийдийн олонлогийг хэрхэн гарсанг ойлгохгүй байж мэднэ. Тэнцэтгэл бишийг бодох үндсэн аргачлал бол тэнцэтгэл бишийн тэмдгийн аль нэг талд тэг үлдээгээд нөгөө талыг тэгтэй тэнцүүлэн тэгшитгэл болгон бодоод тэмдгийн шинжилгээ буюу интервалын аргаар шийдийг тодорхойлох байдаг. Энэ аргачлалаар бид анхдагч тэнцэтгэл бишийг
тэнцэтгэл биш үүснэ. Тэнцэтгэл бишийн шийдийн олонлогийг хэрхэн гарсанг ойлгохгүй байж мэднэ. Тэнцэтгэл бишийг бодох үндсэн аргачлал бол тэнцэтгэл бишийн тэмдгийн аль нэг талд тэг үлдээгээд нөгөө талыг тэгтэй тэнцүүлэн тэгшитгэл болгон бодоод тэмдгийн шинжилгээ буюу интервалын аргаар шийдийг тодорхойлох байдаг. Энэ аргачлалаар бид анхдагч тэнцэтгэл бишийг 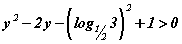 хэлбэрт шилжүүлсэн байгаа. Одоо
хэлбэрт шилжүүлсэн байгаа. Одоо 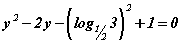 тэгшитгэлийг бодон шийд тоон шулууныг хэдэн интервалд хувааж байгааг тогтоогоод
тэгшитгэлийг бодон шийд тоон шулууныг хэдэн интервалд хувааж байгааг тогтоогоод 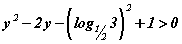 тэнцэтгэл бишийг хангах интервалуудын нэгдлийг л авна.
тэнцэтгэл бишийг хангах интервалуудын нэгдлийг л авна. 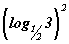 бол тэгээс их ердийн л тоо тул
бол тэгээс их ердийн л тоо тул 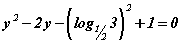 тэгшитгэлд
тэгшитгэлд 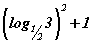 -ийг сул гишүүн гээд цааш өөрсдөө тооцоорой.
-ийг сул гишүүн гээд цааш өөрсдөө тооцоорой.
Орлуулга хийн тооцсоны дараа 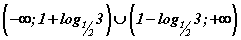 шийдийн олонлог гарснаар анхдагч тэнцэтгэл биш
шийдийн олонлог гарснаар анхдагч тэнцэтгэл биш 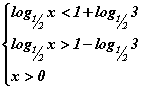 системээр тодорхойлогдоно. Системд тэнцэтгэл бишийн тодорхойлогдох муж
системээр тодорхойлогдоно. Системд тэнцэтгэл бишийн тодорхойлогдох муж 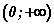 -ийг тооцох ёстойг мартаж болохгүй. Системийг бодъё. Ижил суурьтай логарифмийн
-ийг тооцох ёстойг мартаж болохгүй. Системийг бодъё. Ижил суурьтай логарифмийн 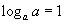 чанар, үржвжрийн
чанар, үржвжрийн 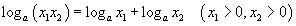 , ногдворын
, ногдворын 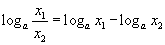 чанаруудаар эхний хоёр тэнцэтгэл бишийг хувиргавал
чанаруудаар эхний хоёр тэнцэтгэл бишийг хувиргавал 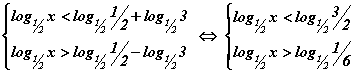 болно. Логарифмийн суурь нэгээс бага тул
болно. Логарифмийн суурь нэгээс бага тул 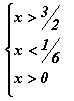 систем гарах бөгөөд анхдагч тэнцэтгэд бишийн шийдийн олонлог
систем гарах бөгөөд анхдагч тэнцэтгэд бишийн шийдийн олонлог 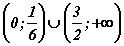 гэж гарна.
гэж гарна.
Санамж: Логарифмийн суурь нэгээс бага байвал тэмдгийг эргүүлэн тавьдаг гэдгийг сурагчид автоматаар цээжилсэн байдаг. Энэ буруу биш ч яагаад ингэж байгаагийн учрыг ойлгосон байх нь чухал. Түүнээс гадна тодорхойлогдох мужийг тооцохгүйгээр бодолтыг хийвэл алдаа гаргахыг санаарай. Логарифмийн зэргүүд 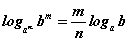 хамааралтай гэдгээс 2-1=1/2 тул
хамааралтай гэдгээс 2-1=1/2 тул 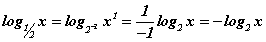 болно. Эндээс
болно. Эндээс 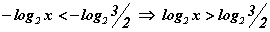 тэнцэтгэл биш үүссэнээр шийд
тэнцэтгэл биш үүссэнээр шийд 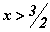 гэж гарч байгааг сайн тогтоон аваарай.
гэж гарч байгааг сайн тогтоон аваарай.
Жич: Манай элсэлтийн ерөнхий шалгалтад иймэрхүү бодлого бараг орж ирдэггүй. Сайт элсэлтийн шалгалтын бэлтгэлээс илүү таныг өөрийгөө хөгжүүлэхэд түлхүү анхаардаг тул бодлого таны мэдлэгт тустай. Бодлого бодоход онолын суурь мэдлэг хичнээн чухал болохыг бодолтоос ойлгосон байх. Онолын хичээлүүдийг сайн судлан ойлговол ямарч төрлийн бодлогын шийдэлд цөөн тооны аргачлал, техникийг ашигладаг нь тодорхой болно. Иймээс хэт олон бодлогын бодолтыг харан цаг алдалгүй эхлээд онолын хичээлүүдийг сайтар судлаад дараа нь бодлогод аргачлалыг хэрхэн ашиглаж байгааг харан эзэмших дадлага хийхийг зөвлөе.
Хариу
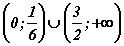





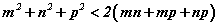 гэдгийг батал
гэдгийг батал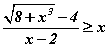 тэнцэл бишийг эмхэтгэж
тэнцэл бишийг эмхэтгэж 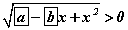 тул орхиж
тул орхиж 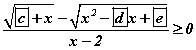 хэлбэрт шилжүүлж шийдийг олбол
хэлбэрт шилжүүлж шийдийг олбол 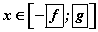 байна.
байна.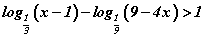 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод. задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.