Конуст ABCD трапецэн суурьтай QABCD пирамидийг багтаажээ. 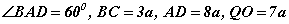 бол (BC, AD - трапецийн сууриуд, QO - пирамидийн өндөр) конусийн хажуу гадаргуун талбай
бол (BC, AD - трапецийн сууриуд, QO - пирамидийн өндөр) конусийн хажуу гадаргуун талбай 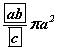 байна.
байна.
Бодолт
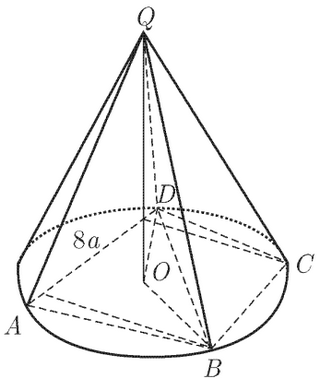 Конусийн хажуу гадаргуун талбайг
Конусийн хажуу гадаргуун талбайг 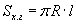 томьёогоор тодорхойлдог. Энд R - суурийн радиус, l - бүрдүүлэгч гэдгийг сануулъя. Талбайг тооцоход шаардлагатай R, l -ийг олъё.
томьёогоор тодорхойлдог. Энд R - суурийн радиус, l - бүрдүүлэгч гэдгийг сануулъя. Талбайг тооцоход шаардлагатай R, l -ийг олъё.
Конуст пирамид багтсан, пирамидийн суурь ABCD трапецийн хажуу талууд тэнцүү гэдгээс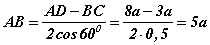 байна. Бодлогын нөхцөл, косинус функцийн тодорхойлолтоор AB -г олж байгаа өөрсдөө ухан ойлгоорой. AB -г олсон тул ADB гурвалжингаас косинусийн
байна. Бодлогын нөхцөл, косинус функцийн тодорхойлолтоор AB -г олж байгаа өөрсдөө ухан ойлгоорой. AB -г олсон тул ADB гурвалжингаас косинусийн 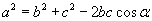 теоремоор
теоремоор 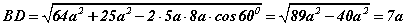 гэж гарна. BOD төв өнцөг тойрогт багтсан BAD өнцгүүд багтсан өнцгийн теоремоор
гэж гарна. BOD төв өнцөг тойрогт багтсан BAD өнцгүүд багтсан өнцгийн теоремоор 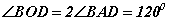 харьцаатай байна. Эндээс
харьцаатай байна. Эндээс 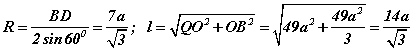 гэж гарна.
гэж гарна.
R, l -ийг олсон тул конусийн хажуу гадаргуун талбай 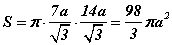 гэж гарснаар a=9; b=8; c=3 байна.
гэж гарснаар a=9; b=8; c=3 байна.
Жич: Бодлого бодох ажиллагаанд таныг илүү түлхүү оролцуулах үүднээс бодолтыг хэрэгээр хураангуй болгосон. R, l -ийг олж байгаа аргыг зураг болон нөхцлийг тооцоод нэмэлт байгуулалт хийн нарийвчлан тооцож бодолтыг ойлгохыг хичээгээрэй. Бүх зүйлийг тайлбарлаад байвал танд үлдэх зүйл бага. Бодолтыг ойлгох хүртлээ давтан үзээрэй.
Хариу
a=9; b=8; c=3





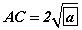
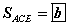
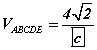
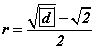 байна.
байна.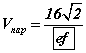 байна.
байна. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.