Зэрэгцээ орших ирмэгүүд нь оройдоо 60° өнцөг үүсгэсэн 3 өндөртэй зөв дөрвөн өнцөгт пирамидын эзэлхүүн 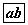 тэнцүү.
тэнцүү.
Бодолт
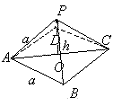 Зөв пирамид зэрэгцээ орших ирмэгүүд оройдоо 60° өнцөг үүсгэж байгаа болохоор пирамидын тал нь a талтай адил талт гурвалжин байна. Пифагорын теоремоор пирамидын өндөр, ирмэг, суурийн диагналын хагасын харьцааг олбол.
Зөв пирамид зэрэгцээ орших ирмэгүүд оройдоо 60° өнцөг үүсгэж байгаа болохоор пирамидын тал нь a талтай адил талт гурвалжин байна. Пифагорын теоремоор пирамидын өндөр, ирмэг, суурийн диагналын хагасын харьцааг олбол. 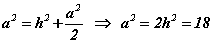 Эндээс
Эндээс 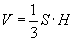 томьёогоор пирамидын эзэлхүүн
томьёогоор пирамидын эзэлхүүн 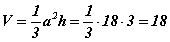
Хариу
a=1; b=8;





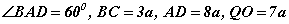 бол (BC, AD - трапецийн сууриуд, QO - пирамидийн өндөр) конусийн хажуу гадаргуун талбай
бол (BC, AD - трапецийн сууриуд, QO - пирамидийн өндөр) конусийн хажуу гадаргуун талбай 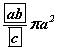 байна.
байна.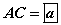 байна.
байна.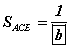
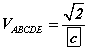 байна.
байна.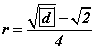 байна.
байна.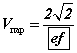 байна.
байна. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.