3x1y5z тоо 36 -д хуваагддаг бол x, y цифрүүдийн нийлбэрийн хамгийн их утгыг олоорой.
Бодолт
Тооны хуваагдах чанарыг мэдэж байхад бодлогыг амархан бодох боломжтой. Хуваагдах чанар арифметикийн сэдэв болохоор мартсан байх тохиолдол их байдгаас ийм төрлийн бодлого хүндрэл учруулах өндөр магадлалтай. Бодлогыг бодохын өмнө 36 -д хуваагдах тооны чанарыг тогтоох хэрэгтэй. 36 -г 6*6, 4*9, 2*18, 3*12 үржвэрээр задалж болно. Анхны тоон үржигдхүүнд задлаад бүх боломжийг гаргаж болно. Бидэнд хамгийн тохирох үржвэр бол 4*9. Учир нь өгөгдсөн тооны сүүлийн цифр бас үл мэдэгдэгч байгаа. Үүнийг ашиглахад бидэнд 4 хамгийн тохиромжтой тоо. Одоо өгөгдсөн тоо 4 ба 9 -д хуваагдаж байвал 36 -д хуваагдана. Хуваагдах шинжийн дагуу тоо 4 -д хуваагдахын тулд түүний сүүлийн 2 цифрээр бүрдсэн тоо 4 хуваагдаж байх нөгөө талаас тоо 9 -д хуваагдахын тулд түүний цифрүүдийн нийлбэр 9 хуваагдаж байх хэрэгтэй. Эндээс 5z тоо 4 хуваагдана. 3+x+1+y+5+z тоо 9 -д хуваагдах ёстой. Энд 2 тохиолдол байна.
1 -р тохиолдол
z=2 байхад 52 дөрөвт хуваагдана гэдгээс 11+x+y нийлбэр 9 -д хуваагдах хэрэгтэй. Энд x+y=7; x+y=16 гэсэн хоёр хувилбар байна.
2 -р тохиолдол
z=6 байхад 56 дөрөвт хуваагдана гэдгээс 15+x+y нийлбэр 9 -д хуваагдах хэрэгтэй. Энд x+y=3; x+y=12 гэсэн хоёр хувилбар байна.
Энд хоёр цифрийн нийлбэр 18 -аас хэтрэхгүй гэдгийг үндэслэж байгааг ойлгоорой. Өгөгдсөн тоо 4 болон 9 -д хуваагдаж байх нөхцлийг хангах x+y нийлбэрийн хамгийн их утга 16 болж байна.
Хариу
16





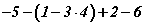 илэрхийллийн утга хэд вэ?
илэрхийллийн утга хэд вэ?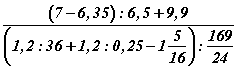 утгыг тооц.
утгыг тооц. задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.