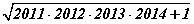илэрхийллийг дөт аргаар бод.
Бодолт
Анхдагч илэрхийллийг A гэж тэмдэглээд x=2011 гэсэн орлуулга хийвэл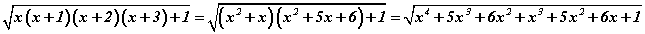 
болно. Гишүүдийг эмхэтгэвэл илэрхийлэл 
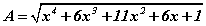хэлбэртэй болно. Эндээс 
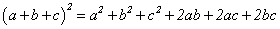томьёогоор 3 гишүүнтийн нийлбэрийн квадрат ялгавал 
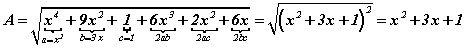гэдгээс 
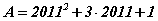гарна.
Хэрвээ 3 гишүүнтийн нийлбэрийн квадратын томьёог санахгүй байвал олон гишүүнтийг олон гишүүнтэд хуваах аргыг ашиглаж болно. Эхний x4 гэдгээс хуваагчийн эхний гишүүн x2 харин хоёрдахь гишүүн бол ax тэгээд 1 буюу хуваагч x2+ax+1 гэсэн хэлбэртэй байна. Үүнээс гадна язгуураас салахын тул бидэнд хуваагчийн квадрат хуваагдагчтай тэнцүү байх хэрэгтэй. Эндээс 6x3 -ийг 2 таслаад хасаж дуусгана гэж үзвэл a=3 байна. Эсхүл x2+ax+1 хэлбэрийн хуваагчаа квадрат зэрэг дэвшүүлэн задлаад дараа нь илэрхийлэлтэй харьцуулан a-г олж болно. Жишээ нь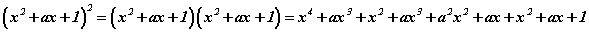 
гэж задлаад хураангуйлбал 
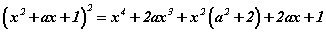гэдгээс a=3 гэж олно.
Жич: Дээрх аргууд бол бичгийн шалгалтанд илүү хэрэгтэй. Харин тестийн хувьд x=2011 гэсэн орлуулга хийхээ харсан бол хариунаас шууд сонгох боломжтой. Дандаа нэмэгдэх байдлаар задрах тул x=2011 гэж сонгох нь амар.
Хариу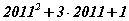
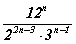бутархайг хураангуйл.
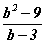бутархайг хураа.
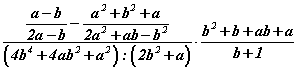илэрхийллийг хялбарчил.
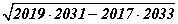илэрхийллийн утгаас ихгүй хамгийн их бүхэл тоог ол.
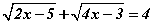тэгшитгэл бод.
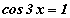тэгшитгэл бод.
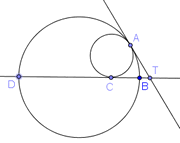Зурагт өгөгдсөн дотоод байдлаараа шүргэлцсэн хоёр тойргийн TA нь ерөнхий шүргэгч, TC нь том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. DC=3, CB=2 бол TA -г ол.