Бүх ирмэг нь 1 урттай байх ABCDE зөв дөрвөн өнцөгт пирамид өгөгдөв.
I. Суурийн диагональ 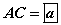 байна.
байна.
II. Диагональ огтлолын талбай 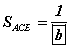
III. Пирамидын эзэлхүүн 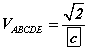 байна.
байна.
IV. Пирамидад багтсан бөмбөрцгийн радиус 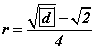 байна.
байна.
V. Энэ пирамидад хамгийн их эзэлхүүнтэй, 4 орой нь хажуу ирмэг дээр, 4 орой нь суурь дээр орших тэгш өнцөгт параллелопепидийн эзэлхүүн нь 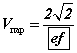 байна.
байна.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах




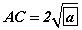
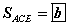
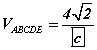
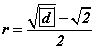 байна.
байна.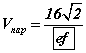 байна.
байна.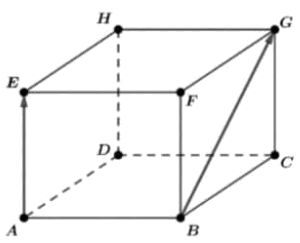 Зурагт өгсөн паралелепидедээс
Зурагт өгсөн паралелепидедээс 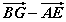 ялгавар вектортэй тэнцүү векторыг ол.
ялгавар вектортэй тэнцүү векторыг ол.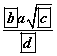 байна.
байна. функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол. тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.