2(x-3)+5(1-x)≥3(2x-5) тэнцэтгэл бишийг бод.
Бодолт
Энгийн тэнцэтгэл биш. Хаалтыг нээвэл 2x-6+5-5x≥6x-15 болно. Цааш гишүүдийг тэмдгийн хоёр талд гаргавал 2x-5x-6x≥-15+6-5 гэдгээс анхны тэнцэтгэл биштэй эн чацуу -9x≥-14 тэнцэтгэл биш үүснэ. Тэнцэтгэл бишийн хоёр талыг сөрөг тоонд хуваах эсхүл үржвэл түүний тэмдэг эсрэг болно гэсэн дүрэм бий. Тэнцэтгэл бишийн бодолтод ихээр хэрэглэдэг дүрэм тул сайн тогтоож аваарай. Ойлгоход ч энгийн хэрвээ -9x≥-14 тэнцэтгэл бишийн гишүүдийг тэмдэгийн хоёр талд гаргавал 14≥9x тэнцэтгэл биш үүснэ. Энэ бол -9x≥-14 тэнцэтгэл бишийн хоёр талыг -1 -ээр үржүүлэх эсхүл хуваасантай ижил. Дүрмийн дагуу -9x≥-14 тэнцэтгэл бишийн хоёр талыг -1 -ээр үржүүлэх эсхүл хуваавал гишүүд эсрэг тэмдэг аваад харин тэмдэг ≥ -ийн эсрэг ≤ тэмдэг болсноор 9x≤14 тэнцэтгэл биш болох ёстой. Сүүлийн тэнцэтгэл бишийг 14≥9x гэж бичихэд ямарч ялгаа байхгүй. Одоо тэнцэтгэл бишийн хоёр талыг 9 -д хуваавал анхны тэнцэтгэл биштэй эн чацуу 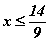 тэнцэтгэл биш гарна. Эндээс өгөгдсөн тэнцэтгэл бишийн шийдийн олонлог
тэнцэтгэл биш гарна. Эндээс өгөгдсөн тэнцэтгэл бишийн шийдийн олонлог 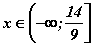 гэж гарна.
гэж гарна.
Хариу
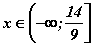





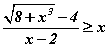 тэнцэл бишийг эмхэтгэж
тэнцэл бишийг эмхэтгэж 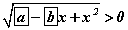 тул орхиж
тул орхиж 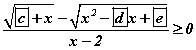 хэлбэрт шилжүүлж шийдийг олбол
хэлбэрт шилжүүлж шийдийг олбол 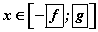 байна.
байна.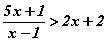 тэнцэл бишийг хангах x -ийн эерэг бүхэл утга хэд байх вэ?
тэнцэл бишийг хангах x -ийн эерэг бүхэл утга хэд байх вэ?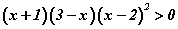 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод. задаргааны хамгийн их нэмэгдхүүн
задаргааны хамгийн их нэмэгдхүүн  бол a, b, c -г ол.
бол a, b, c -г ол. тэгшитгэлийг бод.
тэгшитгэлийг бод. функцийн уламжлалын
функцийн уламжлалын  утгыг ол.
утгыг ол.