Аливаа зүйлийг сурахад таниас нилээдгүй тэсвэр тэвчээр, хичээл зүтгэл, сахилга батыг шаардана. Хүмүүс мөнгө төлчихвөл сурчихдаг гэж бодоод байдаг бололтой. Мөнгө төлөөд хоол унд, хувцас хунар, эд хөрөнгийг шууд авч болохоос мэдлэг, боловсрол, ур чадварыг авахгүй. Үүнийг сайтар эрэгцүүлэн бодоорой. Үүнээс гадна ямарч зүйлийг сурах суурь бол сэтгэн бодох, дүн шинжилгээ хийх, тасралтгүй суралцах юм. Сайтад тавигдаж буй материалууд танд энэхүү суурийг олон авахад л туслах зорилготой. Сурах суурийг тавихад математик, шатар маш том үүрэгтэй гэдгийг хүн төрөлхтөний түүх баталсан зүйл тул бүх хүмүүс бүр багаасаа үүнд суралцах хэрэгтэй гэж бодогдоно.
Энэ удаад шатрын онолчдын дунд томоохон байр суурьтай А. Нимцович боловсруулан, хөгжүүлсэн хамгаалалтын системийн жишээ өргүүдээс үргэлжлүүлэн танилцуулъя. Хамгаалалт бэрсний гамбитийн эсрэг маш сайн үр дүнтэй байгуулалтыг үүсгэдэг гэдэг нь өргүүдээс харагдана.
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах




 тэгшитгэлийг бод.
тэгшитгэлийг бод.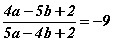 бол
бол 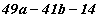 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.