Тэнцүүгийн (=) тэмдгээр холбогдсон хоёр тоон эсхүл үсгэн илэрхийлэл тэнцлийг бүрдүүлнэ. Тэнцүүгийн (=) тэмдгийн зүүн орших илэрхийллийг зүүн буюу нэгдүгээр харин баруун орших илэрхийллийг баруун буюу хоёрдахь хэсэг гэнэ.
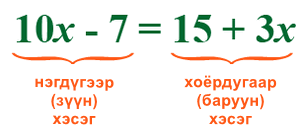
Тэнцлийн хэсгүүдийн байрыг сольж болно. Жишээ нь дээрх 10x-7=15+3x тэнцлийн хэсгүүдийн байрыг солин 15+3x=10x-7 гэж бичиж болно. Тэнцэл адитгал, тэгшитгэл гэсэн хоёр төрөлд худаагдана.
Тэнцлийн шинжүүд
Бүх тэнцлүүд хувиргалт, тэгшитгэлийн бодолтууд сууриладаг хоёр шинжтэй.
- Тэнцлийн хоёр талыг нэг ижил тоо эсхүл алгебрийн илэрхийллээр нэмэгдүүлэх эсхүл багасгахад тэнцэл чанараа буюу тэнцүү байдлаа алдахгүй. Жишээ нь a = b тэнцэл a + m = b + m болон a - m = b - m тэнцлүүдтэй эн чацуу.
- Тэнцлийн хоёр талыг нэг ижил тоо эсхүл алгебрийн илэрхийллээр үржүүлэх эсхүл хуваахад тэнцэл чанараа буюу тэнцүү байдлаа алдахгүй. Жишээ нь a = b тэнцэл am = bm эсхүл a/m = b/m тэнцлүүдтэй эн чацуу.
тэнцэл бишийг бод.
илэрхийллийн хялбарчил.