Аман дугаарлалт гэдэг нь тоонуудыг үгээр илэрхийлэх юм.
Тоонуудын нэрийг мэдэж байхад ямарч зүйлийг тоолох боломжтой. Бичиг мэдэхгүй, тоонуудын тэмдэглэгээг мэдэхгүй ч хүүхдүүд аман дугаарлалтыг маш эрт сурдаг. Өөрөөр хэлбэл амаар тоолох юм.
Нэгээс арав хүртэлх тоолох
Тооллогын нэгжээр одыг ашиглая. Бидэнд хайрцагт одны дүрсүүд байгаа гэж үзээд хайрцагт хичнээн дүрс байгааг тоолоё. Үүнийг хийхийн тулд хайрцагнаас однуудыг дараалуулан аваад авсан дүрсүүдийн тоог нэрлээд байх болно.
| Тооны нэр | Нэгжийн тоо | Тодорхойлолт |
| нэг |  |
Тооллогод ганцыг ширхэг зүйлийг нэг гэж хэлдэг. |
| хоёр |   |
Нэг нэгж дээр дахин нэгийг нэмвэл хоёр нэгж болно. |
| гурав |    |
Байгаа хоёр нэгж дээр хайрцагнаас дахин нэг одыг аван нэмвэл гурав болно. |
| дөрөв |     |
Гурван нэгж дээр дахин нэгийг нэмвэл дөрөв болно. |
| тав |      |
Дөрвөн нэгж дээр дахин нэгийг нэмвэл тав болно. |
| зургаа |       |
Таван нэгж дээр дахин нэгийг нэмвэл зургаа болно. |
| долоо |        |
Зургаан нэгж дээр дахин нэгийг нэмвэл долоо болно. |
| найм |         |
Долоон нэгж дээр дахин нэгийг нэмвэл найм болно. |
| ес |          |
Найман нэгж дээр дахин нэгийг нэмвэл ес болно. |
| арав |           |
Есөн нэгж дээр дахин нэгийг нэмвэл арав болно. |
Ингэснээр хайрцагт дахь однуудыг нэг нэгээр авснаар арван од байгааг тооллоо.
Арван нэгээс хорь хүртлэх тоолол
Хайрцагт үлдсэн однуудыг үргэжлүүлэн тоолоё. Однуудыг ээлж дараагаар аван өмнө тоолсон арван нэгж дээр нэгийг нэмэх замаар дараагийн арван тооны нэрийг гаргавал
| Тооны нэр | Нэгжийн тоо |
| арван нэг |            |
| арван хоёр |             |
| арван гурав |              |
| арван дөрөв |               |
| арван тав |                |
| арван зургаа |                 |
| арван долоо |                  |
| арван найм |                   |
| арван ес |                    |
| хорь |                     |
болно. Одоо бид хорин од буюу хоёр аравтыг тооллоо.
Эндээс тоонуудын нэрийг аравтын нэрэнд "н" дагавар залгаад үүсэх нэрийн араас нэгдүгээр аравтын нэгжийн нэрийг нэмэх дүрмээр гаргаж байгаа нь харагдана.
Хориос зуу хүртлэх тооллого.
Хайрцагнаас однуудыг ээлж дараалан авч хориос цааш тоолохдоо дээрх дүрмийн дагуу хоёр аравт буюу хорь нэрэнд "н" дагавар залгаад үүсэх нэрийн араас нэгдүгээр аравтын нэгжийн нэрийг нэмвэл
- хорин нэг
- хорин хоёр
- хорин гурав
- хорин дөрөв
- хорин тав
- хорин зургаа
- хорин долоо
- хорин найм
- хорин ес
- гуч буюу гурван аравт
гэж тоологдоно. Зуу бол арван аравт бөгөөд аравтуудын нэрүүд
- нэг аравт - арав
- хоёр аравт - хорь
- гурван аравт - гуч
- дөрвөн аравт - дөч
- таван аравт - тавь
- зургаан аравт - жар
- долоон аравт - дал
- найман аравт - ная
- есөн аравт - ер
- арван аравт - зуу
байдаг. Аравтуудын нэрийг мэдэн тооны нэрийг зохиох дүрмийн баримталбал тооллогыг хэд хүртэл хийх боломжтой.





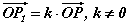 гэсэн P1 цэгээр илэрхийлэгдэх хувиргалт юм.
гэсэн P1 цэгээр илэрхийлэгдэх хувиргалт юм. тэгшитгэлийг бод.
тэгшитгэлийг бод.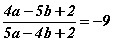 бол
бол 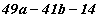 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.