Теорем, аксиом, тодорхойлолт
Баталгаа - Ямар нэгэн шинж чанарыг тогтоохыг хэлэлцэх.
Теорем - Баталгаа шаардсан ямар нэгэн шинж чанарыг тогтоохыг нотлох. Теоремуудыг бас лемм, шинж, үр дагавар, дүрэм, чанар, нотолгоо гэж нэрлэдэг. Теоремыг өмнө нь тогтоосон шинжүүдийг үндэслэн баталдаг. Геометрт зарим шинж чанарыг үндсэн гэж үзэж баталгаа шаардахгүй хэрэглэдэг.
Аксиом - Баталгаагүйгээр ашигладаг зарим шинж чанарыг тогтоосон нотолгоо. Аксиом нь туршилтаас үүсдэг бөгөөд туршилт нь тэдгээрийн үнэнийг бүхэлд нь тогтооно.Янз бүрийн аргаар аксиомуудыг зохиож болно. Гэхдээ аксиом нь геометрийн бусад шинж чанарыг батлахад хангалттай байх хэрэгтэй. Нэг аксиомыг нөгөөгөөр соливол энэ нь теорем болж байгаа тул түүнийг батлах хэрэгтэй болдог.
Үндсэн ойлголтууд - Геометрт / ер нь математикт / утга бүхий тодорхойлолт өгч болдоггүй ойлголтууд байдаг. Эдгээрийг үндсэн ойлголтууд гэнэ. Ийм ойлголтуудын утгыг туршилтын үндсэн дээр л тогтоодог. Цэг болон шулуун шугам нь үндсэн ойлголтууд юм. Үндсэн ойлголтоос үндэслэн бид бусад ойлголтод тодорхойлолт өгч чадна.
Шулуун, цацраг, хэрчим
Шулуун шугамыг хоёр тал руу нь хязгааргүй үргэлжлүүлж болно. Бид шулууныг төгсгөлгүй гэж үздэг. Нэг талаасаа эхлэлтэй нөгөө тал нь хязгааргүй үргэлжлэх шулуун шугамыг цацраг гэнэ.
Хоёр талаасаа хязгаарлагдсан шулуун шугамын хэсгийг хэрчим гэнэ.





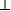 AB ба AO = OB гэе
AB ба AO = OB гэе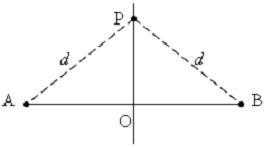
 тэгшитгэлийг бод.
тэгшитгэлийг бод.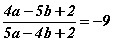 бол
бол 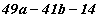 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.