Тэмдэглэгээ
a, b, c - талууд, A, B, C - өнцгүүд, p=(a+b+c)/2 - хагас периметр, h - өндөр, S - талбай, R - багтаасан тойргийн радиус, r - багтсан тойргийн радиус.
Косинусын теорем
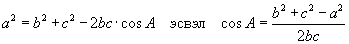
Синусын теорем
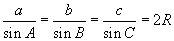
Тангенсын теорем
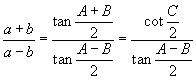
Талбайн томьёо
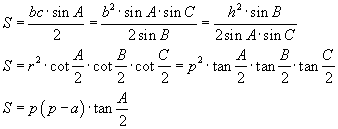
Героний томьёо
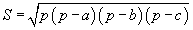
Багтаасан ба багтсан тойргийн радиус
Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.
Нээгдсэн тоо: 8879 Нийтийн
Математикийн бодлого бодох яагаад хүнд байдаг вэ? гэвэл энд бүх зүйлийг ямар нэгэн алдаа гаргахгүй хийх хэрэгтэй болдог. Алдаа гаргавал тэр дороо алдаа гэж мэдэгдэхгүй та зүгээр л өөр бодлого бодох ажиллагаанд шилжээд явдаг. Тэгвэл бодлого биш жишээ нь гадаад хэл, уран зохиол, нийгмийн чиглэлийн асуудлыг буруу зөрүү явсан байсан ч зөв замдаа шууд ороод шийдэх боломжтой. Харин бодлого бодоход ийм зүйл байхгүй. Алдаа л хийсэн бол буруу зам руу орно. Үүнийгээ мэдэхгүй бол алдаа болно мэдвэл бараг эхнээс нь шалгах хэрэгтэй болно.
Нээгдсэн тоо: 3966 Төлбөртэй
Тойрог болон шулуунуудын харилцан байршлаар огтлогч, шүргэгч гэсэн чухал ухагдхуунууд үүсдэг. Эдгээрийг сайн ойлгон шинжүүдийг мэдэж байхад тойрогтой холбоотой олон тооны бодлогыг шийдэх суурь болдогийг сануулъя. Хавтгайд тойрог болон шулуунууд огтлолцон эсхүл огтлолцохгүйгээр байрлах боломжтой.
Тойрогийн төв O -гоос m шулуун хүртлэх зай OA перпендикулярийн урттай тэнцүү. Эндээс тойргийн төвөөс шулуун хүртлэх зай нь тойргийн төвөөс шулуунд буулгасан перпендикулярийн урттай тэнцэнэ. Энэ зайнаас хамааран тойрог шулууны байрлалыг тодорхойлох боломжтой.
Нээгдсэн тоо: 3929 Бүртгүүлэх
Тэгш өнцөгт гурвалжны талуудын харьцааг хурц өнцгийн тригнометрийн функцүүд гэдэг. / Зур. 2 /
Нээгдсэн тоо: 9569 Нийтийн
Прогресстой холбоотой бодлогууд элсэлтийн ерөнхий шалгалтанд ирэх нь бараг уламжлал. Бид энэ хичээлээр прогресстой хамааралтай бодлогуудын талаар авч үзэх болно. Үндсэн ойлголтыг Арифметик ба геометр прогресс хичээлээс аваарай. Прогрессын бодлогуудыг бодоход холбогдох томьёонуудыг мэдэж байхад тийм хүнд биш. Тригнометрийн тэгшитгэл, алгебрийн тэгшитгэл, илэрхийлэл хялбарчлах гэх мэтийн бодлогыг бодох тогтсон аргачлал, дүрэм байдаг бол прогресстой холбоотой бодлогыг бодох тодорхой аргачлалууд гэж байдаггүй бодлогын нөхцөлд тулгуурлан томьёогоо ашиглаад явдаг.
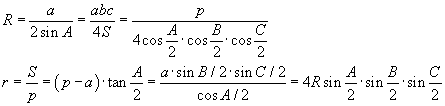
илэрхийллийг хялбарчил.