Функцын гүдгэр, хотгор ба муруйлтын цэг

Хэрвээ f(x) функцын уламжлал 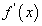нь x0 цэгт дифференциалчлагдаж байвал түүнийг f(x) функцын x0 цэг дээрх хоёрдугаар эрэмбийн уламжлал / 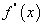гэж тэмдэглэнэ./ гэнэ.

  1. Хэрвээ функцын график нь дурын 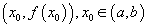цэгт y=f(x) функцын графикийн муруйд татсан шүргэгчийн доор байрлаж байвал f(x) функцыг (a,b) интервалд гүдгэр гэнэ.
  2. Хэрвээ функцын график нь дурын 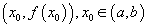цэгт y=f(x) функцын графикийн муруйд татсан шүргэгчийн дээр байрлаж байвал f(x) функцыг (a,b) интервалд хотгор гэнэ.

Материалыг бүртгэлтэй хэрэглэгч үзнэ.

how_to_regБүртгүүлэх

Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.

Холбоотой материалууд
Магадлалын тодорхойлолт үндсэн шинжүүд

  Нээгдсэн тоо: 9972 Нийтийн

Магадлалын аксиом тодорхойлолт

Эгэл үзэгдлүүдийн олонлог E өгөгдсөн ба үзэгдэл бүрт :

  • P(A)≥0
  • хос харш үзэдлүүдийн хувьд:  тэнцэл биелнэ,
  • P(E)=1

харгалзсан цорын ганц P(A) тоо байна гэж үзье. Тэгвэл E олонлогийн үзэгдлүүдэд магадлал байна. P(A) тоог A үзэгдлийн магадлал гэж хэлнэ.

Тооноос куб язгуур авах

  Нээгдсэн тоо: 17848 Нийтийн

Бид өмнө нь Тооноос квадрат язгуур авах талаар үзсэн бол энэхүү нийтлэлээр тооны машин ашиглахгүйгээр куб язгуур авахыг сурцгаах болно. Энд бид зөвхөн натурал тоонуудын хувьд авч үзнэ.

Дээрх тоонуудын язгуурыг цээжээр гаргана гэвэл та хир их хугацаа зарцуулна гэж бодож байна. Хэрвээ та бидний үзэх аргачлалыг хэдэн удаа сайн давтвал ямарч тооны куб язгуурыг тун бага хугацаанд гаргах болно.

Гурвалжны периметр, талбай

  Нээгдсэн тоо: 26675 Нийтийн

Хаалттай тахир шугаман дүрсүүд периметр, талбайтай байдаг. Гурвалжин ч хаалттай тахир шугамаар үүсдэг дүрс тул хичээлээр гурвалжны периметр, талбайн талаар авч үзье.

Жич: Геометрийн бодлогод периметр, талбайг ол гэсэн нөхцөл байхаас тухайн ухагдхуун гэж юу болох хэрхэн тооцохыг та өөрөө мэдэж байхыг шаардана. Ухагдхууныг мэдэхгүй, яаж тооцохыг мэдэхгүй бол бодлогыг бодохгүй л гэсэн үг.

Биетийн өнцөгүүд

  Нээгдсэн тоо: 2637 Нийтийн

Битүүрсэн чиглүүлэгчтэй шовгор гадаргуун зурвасаар хязгаарлагдсан огторгуйн хэсгийг биетийн өнцөг гэнэ. Биетийн өнцөг нь бөөрөнхий гадаргуун (ABCDEF) /Зур. 98/ хэсгээр хэмжигдэнэ.

Биетийн өнцгийг (ABCDEF) талбай, шаарын радиусын квадратын харьцаагаар хэмжинэ.

Лямбда

Лямбда-илэрхийлэл нь нэргүй аргын хураангуй бичилтийг илэрхийлнэ. Лямбда-илэрхийлэл утга буцаадаг, буцаасан утгыг өөр аргын…

Нээгдсэн тоо : 66

 
Outlet компонент

Кодийн сайжруулалт /рефакторинг/ хичээлээр програмийн кодоо react -ийн зарчимд нийцүүлэн компонентод салгасан.…

Нээгдсэн тоо : 95

 
Хадгалагч (Memento)

Хадгалагч (Memento) хэв обьектын дотоод төлвийг түүний гадна гаргаж дараа нь хайрцаглалтын зарчмыг зөрчихгүйгээр обьектыг сэргээх боломжийг олгодог.

…

Нээгдсэн тоо : 101

 
Нэргүй арга

Делегаттай нэргүй арга нягт холбоотой. Нэргүй аргуудыг делегатийн хувийг үүсгэхэд ашигладаг.
Нэргүй аргуудын тодорхойлолт delegate түлхүүр үгээр…

Нээгдсэн тоо : 124

 
Урвуу матриц

Математикт харилцан урвуу тоонууд гэж бий. Ямар нэгэн тооны урвуу тоог олохдоо тухайн тоог сөрөг нэг зэрэг дэвшүүлээд…

Нээгдсэн тоо : 125

 
Кодийн сайжруулалт

Төсөлд react-router-dom санг оруулан чиглүүлэгчдийг бүртгүүлэн тохируулсан Санг суулган тохируулах хичээлээр бид хуудас…

Нээгдсэн тоо : 179

 
Хуваах

Хуваах нь нэг тоо нөгөө тоонд хэдэн удаа агуулагдаж буй тодорхойлох арифметикийн үйлдэл.
Хуваалтыг нэг бус удаа…

Нээгдсэн тоо : 120

 
Зуучлагч (Mediator)

Зуучлагч (Mediator) нь олон тооны обьектууд бие биетэйгээ холбоос үүсгэхгүйгээр харилцан ажиллах боломжийг хангах загварчлалын хэв юм. Ингэснээр…

Нээгдсэн тоо : 116

 
Делегатийн хэрэглээ

Делегатууд хичээлд ухагдхууны талаар дэлгэрэнгүй үзсэн ч жишээнүүд делегатийн хүчийг бүрэн харуулж чадахааргүй байсан.…

Нээгдсэн тоо : 128

 
Энэ долоо хоногт
Бодлого 9.007

Адил хажуут трапецын сууриуд 20 ба 12 см. Трапецыг багтаасан тойргийн төв их суурь дээр байрлах бол трапецын диагналыг ол.

Нээгдсэн тоо : 1169

 
Бодлого 7.024

тэгшитгэлийн язгууруудын нийлбэрийг ол.

Нээгдсэн тоо : 1089

 
Бодлого 9.129

Зурагт үзүүлсэн хагас тойрогт бол AB -ийн уртыг ол.

Нээгдсэн тоо : 840

 
© 2014 Зохиогчийн эрхээр хамгаалагдсан. Холбогдох - 96655195