Урт хугацааны олон нүүдэлт тэмцлийн эцэст аль нэг тал нь нэг хүүний давуутай хүүний эндшпильд орох нь цөөнгүй байдаг. Ийм багахан хэмжээний материалын давуу тал ялалтанд хангалттай юу? гэсэн асуулт гарч ирнэ. Хүүний төгсгөлийг тоглох зарчим дүрмүүдийг сайтар судалж байж л энэхүү асуултын хариуг олох болно. Юуны өмнө хамгийн бага материалын давуу тал болох ноён ганц хүүтэйгээр ноёны эсрэг хэрхэн тоглохыг эзэмших хэрэгтэй. Онолоор хүчний ийм харьцаа бүхий байрлал 160 гаруй мянгаар тоологдоно. Ийм хязгааргүй далайд хэрхэн баримжаалах вэ? Үнэндээ бол үүний тулд энгийн 2-3 дүрмийг мэдэж байхад л хангалттай.
Эдгээрийн нэг нь олон тооны байрлалд тохирох квадратын дүрэм юм. Дүрмийг хүү ноёны тусламжгүйгээр бэрс гарах гэж оролдоход хэрэглэдэг. 1-р диаграмаар үзүүлсэн байрлалыг авч үзье.
 |
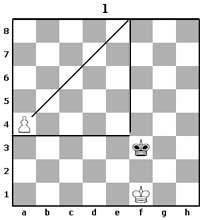Цагаан хүү алдарт a8 нүд рүү тэмүүлж байна. Хар ноён түүнийг барихыг хичээнэ. Эндээс хэн нь энэхүү уралдаанд түрүүлэх вэ? гэсэн асуулт гарч ирнэ.Туршлагагүй шатарчид энэхүү асуултанд би ийшээ, тэр тийшээ, би ийшээ гэх мэтээр тоолж эхэлдэг. Ингэхдээ ийшээ-тийшээ гэсэн тоогоо алдан хэд дахих ч тохиолдол багагүй. Харин туршлагатай шатарчид эцсийн үр дүнг квадратын дүрмээр бараг шууд л тодорхойлдог. Энэхүү дүрмийг тодорхойлбол Сул талын ноён хүүний квадратад эсвэл өөрийн нүүдэлээр энэхүү квадратад орж байвал хүүг барина. Квадратыг сул талын ноён руу дотроо бодон дараах байдлаар үүсгэнэ. Квадратын талаар хүү бэрс гарах нүд хүртэлх зайг авна. Ингэхдээ хүү болон бэрс гарах нүд нь квадратын буланд байрлана. 1-р диаграмд a4 хүүний хувьд a4-a8-e8-e4 квадрат байна. (a4 - a8 хүртэлх 5 нүд a4 -өөс баруун тийш 5 нүд) Хүү a5 шилжвэл түүний квадрат a5-a8-d8-d5 гэх мэтээр багасна. Ийм квадратыг санаандаа төсөөлөх нь хүнд биш ажил ч түүнийг хураангуйлж болно. Квадратын диагналыг олон харахад хангалттай. (1-р диаграмд a4-e8 шугам болно.) |
Квадратын дүрмийг мэдсэн болохоор 1-р диаграмын байрлалд хэрвээ хар эхэлж нүүх бол тэдний ноён хүүг гүйцэн устгаж чадна. Харин цагаан нүүхээр байсан бол хүү эсрэг ноёнд гүйцэгдэхгүй бэрс болсноор цагаан хожино гэдгийг шууд хэлж чадна. Дээрх баталгааг өөрсдөө хөлөг дээр туршин шалгаарай.
 |
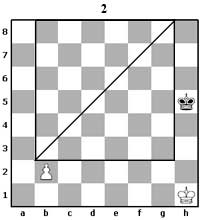Анхны байрлалд байгаа хүү нүд алгасан нүүж болдогийг хүүний квадрат байгуулах үедээ тооцох хэрэгтэй. Жишээ нь 2-р диаграмд үзүүлсэн байрлалд b2 хүүний квадратыг байгуулахдаа b3 хүүнийхтэй ижлээр байгуулна. 2-р диаграмын байрлалд квадратын дүрмээр цагаан болон харын нүүдэлд үр дүн хэрхэн гарахыг өөрсдөө тодорхойлоорой. |
Хөлөг дээрх бусад хүүнүүд нь дүрэмд өөрчлөлт оруулж болно. Жишээ нь 1-р диаграмын байрлалд d5 нүдэнд хар хүүг тавибал хүү өөрийн ноёны замд саад болно. 1... Нe4 2. a5 Нe5 (d5 дээрх хүүг тойрохын тулд цагаан хүүний квадратаас ноён гарч байна.) 3. a6 Нd6 4. a7 Нc7 5. a8Б гээд цагаан хожино.
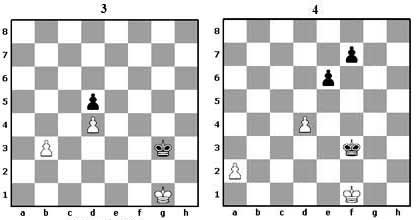
3-р диаграмд өөр нэгэн жишээг үзүүллээ. 1. b4 Нf4 (Ноён хүүний квадратад орлоо. Гэхдээ) 2. b5 хар ноён e5 нүдэнд орох хэрэгтэй боловч цагаан хүү нүдийг хянаж байгаа тул орох боломжгүй. Эндээс b шугамын хүү бэрс гарах нь ойлгомжтой боллоо.
Заримдаа хөөж байгаа ноёнд өрсөлдөгч хэргээр саад бий болгодог. Жишээ нь 4-р диаграмын байрлалд a шугамын хүүг a8 нүд рүү хөдлөхөөс өмнө цагаан эсрэг ноёны замд хаалт тавьж өгч байна. 1. d5! (шууд 1. a4 гэж нүүвэл хүү баригдана гэдгийг шалгаарай) 1. ... ed 2. a4 Нe4 3. a5 цагаан хожино.
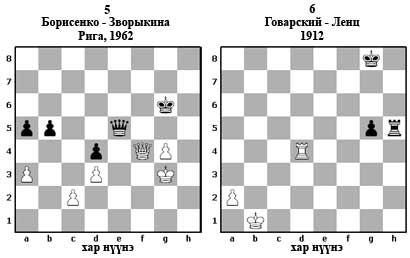
Хичээлийн төгсгөлд практик тохиолдсон хоёр жишээг харъя. 5,6 - р диаграм
5-р диаграмд 38. ... Б:f4+ 39. Н:f4 a4! 40. Нe4 b4 41. Н:d4 b:a3 42. Нc3 Нg5 43. d4 Н:g4 цагаан цугцвангд орон бууж өгсөн.
6-р диаграмд 35. ... Трh7?? 36. Трd8+ Нg7 37. Трd7+ Нg8 38. Тр:h7 Н:h7 39. Нc2! хар бууж өглөө. Цагаан ноён g хүүгийн квадратад орсон байхад түүний хар амидаа a хүүг гүйцэхгүй.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.