Бид захын хүүнүүд хичээлд түлхүүр нүдний тухай ойлголттой танилцсан. Эдгээрийг эзлэн авах нь шатрын тулааны эцсийн үр дүнд нөлөөлдөгийг бид мэднэ. Захын биш нүүргүй хүүнд бас түлхүүр нүднүүд гэж байдаг. Захын биш хүүнүүд нэг биш гурван түлхүүр талбартай байдгаараа захын хүүнээс ялгаатай.
 |
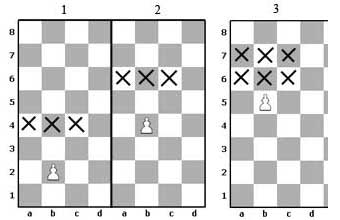1-р диаграмд b2 нүдний хүүний түлхүүр талбаруудыг Х тэмдгээр үзүүлсэн. Эдгээр талбаруудад a4, b4, c4 нүднүүд орно. Хүү урагшаа давшихад түүний түлхүүр талбарууд даган хөдөлнө. b4 хүүний хувьд (2-р диаграм) түлхүүр талбарууд нь a6, b6, c6 болох жишээтэй. Хүү дундаж шугамыг өнгөрөхөд түүний түлхүүр талбар (a6, b6, c6, a7, b7, c7) 6 болдог. (3-р диаграм) |
Материалыг тусгай эрхтэй хэрэглэгч үзнэ.
request_quoteТусгай эрх авах
тэгшитгэлийн язгуурууд x1 , x2 , x3 бол 