Огторгуйн геометр

Дурын призм

(l - хажуу ирмэг, P - периметр, S - суурийн талбай, H - өндөр, Pогт.- перпендикуляр огтлолын периметр, Sогт - перпендикуляр огтлолын талбай, Sх.г - хажуу гадаргуун талбай, V - эзэлхүүн)

�
Дугаар Тодорхойлолт Томьёо
16.1.1 Хажуу гадаргуун талбай
16.1.2 Эзэлхүүн
16.1.3 Эзэлхүүн
16.2.1 Хажуу гадаргуун талбай /Шулуун призм/

Тэгш өнцөгт паралелпепид

(a, b, c - урт, өргөн, өндөр, d - диагнал)

Дугаар Тодорхойлолт Томьёо
16.3.1 Хажуу гадаргуун талбай
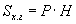16.3.2 Эзэлхүүн
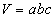16.3.3 Диагнал

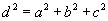Куб

(a - ирмэг)

Дугаар Тодорхойлолт Томьёо
16.4.1 Эзэлхүүн
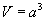16.4.2 Диагнал

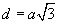Дурын пирамид

Дугаар Тодорхойлолт Томьёо
16.5.1 Эзэлхүүн

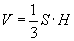Зөв пирамид

(P - периметр, l - апофем, Sх.г - хажуу гадаргуун талбай)

Дугаар Тодорхойлолт Томьёо
16.6.1 Хажуу гадаргуун талбай
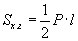16.6.2 Эзэлхүүн

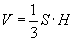Зүсэгдсэн дурын пирамид

(S1 , S2 - сууриудын талбай, h - өндөр, V - эзэлхүүн)

Дугаар Тодорхойлолт Томьёо
16.7.1 Эзэлхүүн

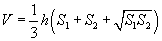Зүсэгдсэн зөв пирамид

(P1 , P2 - сууриудын периметр, l - апофем, Sх.г - хажуу гадаргуун талбай)

Дугаар Тодорхойлолт Томьёо
16.8.1 Хажуу гадаргуун талбай

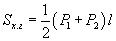Цилиндр

(R - суурийн радиус, H - өндөр, Sх.г - хажуу гадаргуун талбай, V - эзэлхүүн)

Дугаар Тодорхойлолт Томьёо
16.9.1 Хажуу гадаргуун талбай
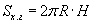16.9.2 Эзэлхүүн

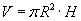Конус

(R - суурийн радиус, H - өндөр, l - бүрдүүлэгч, Sх.г - хажуу гадаргуун талбай, V - эзэлхүүн)

Дугаар Тодорхойлолт Томьёо
16.10.1 Хажуу гадаргуун талбай
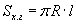16.10.2 Эзэлхүүн

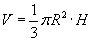Шаар, бөмбөлөг

(R - шаарын радиус, S - бөөрөнхий гадаргуун талбай, V - эзэлхүүн)

Дугаар Тодорхойлолт Томьёо
16.11.1 Хажуу гадаргуун талбай
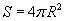16.11.2 Эзэлхүүн

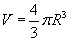Шаарын сегмент

(R - шаарын радиус, h - сегментийн өндөр, S - сегментийн бөөрөнхий гадаргуун талбай, V - эзэлхүүн)

Дугаар Тодорхойлолт Томьёо
16.11.3 Хажуу гадаргуун талбай
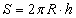16.11.4 Эзэлхүүн

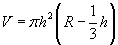Шаарын сектор

(R - шаарын радиус, h - сегментийн өндөр, V - эзэлхүүн)

Дугаар Тодорхойлолт Томьёо
16.11.5 Эзэлхүүн

Мэдээлэл таалагдсан бол найзуудтайгаа хуваалцаарай.

Холбоотой материалууд
Хязгаар

  Нээгдсэн тоо: 8905 Нийтийн

Хязгаар, хязгаарын арифметик үйлдлүүд, хязгаарын чанарууд, чухал хязгаарууд

Тэнцэл биш

  Нээгдсэн тоо: 7670 Нийтийн

Тэнцэл биш, үндсэн чанарууд, бодох томьёонууд

Тригнометр

  Нээгдсэн тоо: 9869 Нийтийн

Тригнометрийн хувиргалтууд хийхэд ашигладаг томьёонууд

Вектор хуурмаг тоо

  Нээгдсэн тоо: 7471 Нийтийн

Вектор

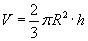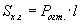
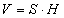
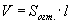
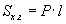
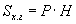
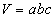
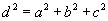
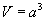
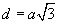
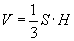
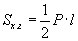
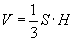
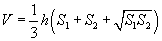
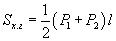
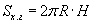
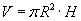
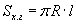
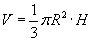
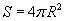
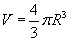
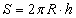
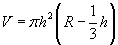
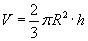
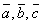m, n - тоонууд, α - хоёр векторын хоорондын өнцөг, - векторууд, 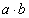- векторуудын скаляр үржвэр, |a| - векторын урт

Outlet компонент

Кодийн сайжруулалт /рефакторинг/ хичээлээр програмийн кодоо react -ийн зарчимд нийцүүлэн компонентод салгасан.…

Нээгдсэн тоо : 7

 
Хадгалагч (Memento)

Хадгалагч (Memento) хэв обьектын дотоод төлвийг түүний гадна гаргаж дараа нь хайрцаглалтын зарчмыг зөрчихгүйгээр обьектыг сэргээх боломжийг олгодог.

…

Нээгдсэн тоо : 15

 
Нэргүй арга

Делегаттай нэргүй арга нягт холбоотой. Нэргүй аргуудыг делегатийн хувийг үүсгэхэд ашигладаг.
Нэргүй аргуудын тодорхойлолт delegate түлхүүр үгээр…

Нээгдсэн тоо : 15

 
Урвуу матриц

Математикт харилцан урвуу тоонууд гэж бий. Ямар нэгэн тооны урвуу тоог олохдоо тухайн тоог сөрөг нэг зэрэг дэвшүүлээд…

Нээгдсэн тоо : 27

 
Кодийн сайжруулалт

Төсөлд react-router-dom санг оруулан чиглүүлэгчдийг бүртгүүлэн тохируулсан Санг суулган тохируулах хичээлээр бид хуудас…

Нээгдсэн тоо : 26

 
Хуваах

Хуваах нь нэг тоо нөгөө тоонд хэдэн удаа агуулагдаж буй тодорхойлох арифметикийн үйлдэл.
Хуваалтыг нэг бус удаа…

Нээгдсэн тоо : 27

 
Зуучлагч (Mediator)

Зуучлагч (Mediator) нь олон тооны обьектууд бие биетэйгээ холбоос үүсгэхгүйгээр харилцан ажиллах боломжийг хангах загварчлалын хэв юм. Ингэснээр…

Нээгдсэн тоо : 25

 
Делегатийн хэрэглээ

Делегатууд хичээлд ухагдхууны талаар дэлгэрэнгүй үзсэн ч жишээнүүд делегатийн хүчийг бүрэн харуулж чадахааргүй байсан.…

Нээгдсэн тоо : 37

 
Нэмэлт санг…

react програмд олон хуудас үүсгэн удирдахын тулд react -ийн бүрэлдхүүнд ордоггүй ч түүнтэй нягт холбоотой ажилладаг нэмэлт пакетийг…

Нээгдсэн тоо : 43

 
Энэ долоо хоногт
Бодлого 15.014

функц өгөгдөв.

  1. f(x) функцын x0=5 абсцисстай M цэгт татсан шүргэгч шулууны тэгшитгэл
  2. f(x) функцын график, дээрх шүргэгч шулуун болон координатын тэнхлэгүүдээр хүрээлэгдсэн дүрсийн талбай  
  3. f(x) функцын графикийг M цэгт шүргэх, төв нь OX (абсцисс) тэнхлэг дээр орших тойргийн тэгшитгэл

Нээгдсэн тоо : 2767

 
Бодлого 2.094

илэрхийллийн a=36,7 тэнцүү байх утгыг ол.

Нээгдсэн тоо : 656

 
Бодлого 3.094

a ба b нь 3x2-x-1=0 тэгшитгэлийн шийдүүдтэй тэнцүү бол илэрхийллийн утгыг ол.

Нээгдсэн тоо : 692

 
© 2014 Зохиогчийн эрхээр хамгаалагдсан. Холбогдох - 96655195