Тэнцэтгэл бишийг бодох бодлого элсэлтийн ерөнхий шалгалтанд орж ирэх нь гарцаагүй. Олон гишүүнт, логарифм, тригнометр, рационал, ирррационал гэх мэтээр тэнцэтгэл бишүүд олон төрлийнх байдаг. Сурагчид тэнцэтгэл биш тэр тусмаа иррационал тэнцэтгэл бишийг бодохдоо тодорхой хүндрэлтэй тулгардаг тул энэ хичээлээр иррационал тэнцэтгэл бишийг бодох тухай авч үзье. Язгуур доор функцыг агуулсан тэнцэтгэл бишийг иррационал тэнцэтгэл биш гэдэг. Хамгийн ихээр тохиолддог иррационал тэнцэтгэл бишийн хэлбэрүүд тэдгээрийн бодолтын талаар авч үзье.
Математикийн бичлэгийг их сайн ойлгож сурах хэрэгтэй шүү. Жишээ нь иррационал тэнцэтгэл бишийн ерөнхий хэлбэрт f(x), g(x) гэх мэтийн бичлэг гараад ирэхээр айгаад сүрдээд байх юм байхгүй. Энэ бол зүгээр л хаалтан доторх хувьсагчаас хамаарсан ямар нэгэн функцыг зааж байгаа юм, Жишээлбэл x2, x3+2x2+3x-5, sinx гэх мэтээр. Ийм бичлэгүүдийг ерөнхий байдлаар f(x), g(x) гэх мэтээр бичиж байгаа юм.
Хэрвээ g(x) тогтмол байвал тэнцэтгэл биш маш энгийн болдог. Хичээлээр авч үзэх тэнцэтгэл бишүүдийн төрлүүд хэлбэр талаасаа их адилхан мэт боловч бодолтын аргачлал нь зарчмын зөрүүтэй байдгийг анхаарна уу.
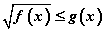 хэлбэрийн тэнцэтгэл биш
хэлбэрийн тэнцэтгэл биш
Ийм төрлийн тэнцэтгэл бишүүд энгийн болоод ойлгомжтой. Тэнцэтгэл бишийн тэмдэг бага эсвэл бага буюу тэнцүү гэж байж болно. Дээрх тэнцэтгэл бишийн хувьд доорх гаргалгаа хүчинтэй.
Теорем.
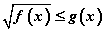 хэлбэрийн ямарч иррационал тэнцэтгэл биш нь
хэлбэрийн ямарч иррационал тэнцэтгэл биш нь 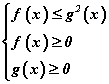 гэсэн тэнцэтгэл бишүүдийн системтэй эн чацуу.
гэсэн тэнцэтгэл бишүүдийн системтэй эн чацуу.
Яагаад ийм системтэй эн чацуу болохыг авч үзвэл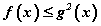 - Анхдагч тэнцэтгэл бишийн хоёр талыг квадрат зэрэг дэвшүүлсэн байгаа энэ тэнцэтгэл биш ойлгомжтой. Гэхдээ тэнцэтгэл бишийн хоёр тал хоёулаа сөрөг биш байхад л эн чацуу чанарыг хадгалан квадрат дэвшүүлэх боломжтой. Хоёр тал нь сөрөг эсхүл өөр тэмдэгтэй тэнцэлгэл бишийг квадрат дэвшүүлэхэд анхдагч тэнцэтгэл биштэй эн чацуу эсхүл эн чацуу биш тэнцэтгэл биш гарах боломжтой. Үүнийг тоон тэнцэтгэл биш дээр шалган харуулъя. Жишээ нь –1 < 3 бол зөв тэнцэтгэл биш. Хоёр талыг квадрат дэвшүүлбэл 1 < 9 гэсэн бас зөв тэнцэтгэл биш гарна. Харин –4 < –1 гэсэн зөв тэнцэтгэл бишийн хоёр талыг квадрат зэрэг дэвшүүлбэл 16 < 1 гэсэн буруу тэнцэтгэл биш болон хувирна. Эндээс үүдэн нөгөө хоёр тэнцэтгэл биш гарч байгаа юм.
- Анхдагч тэнцэтгэл бишийн хоёр талыг квадрат зэрэг дэвшүүлсэн байгаа энэ тэнцэтгэл биш ойлгомжтой. Гэхдээ тэнцэтгэл бишийн хоёр тал хоёулаа сөрөг биш байхад л эн чацуу чанарыг хадгалан квадрат дэвшүүлэх боломжтой. Хоёр тал нь сөрөг эсхүл өөр тэмдэгтэй тэнцэлгэл бишийг квадрат дэвшүүлэхэд анхдагч тэнцэтгэл биштэй эн чацуу эсхүл эн чацуу биш тэнцэтгэл биш гарах боломжтой. Үүнийг тоон тэнцэтгэл биш дээр шалган харуулъя. Жишээ нь –1 < 3 бол зөв тэнцэтгэл биш. Хоёр талыг квадрат дэвшүүлбэл 1 < 9 гэсэн бас зөв тэнцэтгэл биш гарна. Харин –4 < –1 гэсэн зөв тэнцэтгэл бишийн хоёр талыг квадрат зэрэг дэвшүүлбэл 16 < 1 гэсэн буруу тэнцэтгэл биш болон хувирна. Эндээс үүдэн нөгөө хоёр тэнцэтгэл биш гарч байгаа юм. 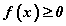 - Язгуурын тодорхойлогдох муж. Зөвхөн эерэг тооноос арифметикийн квадрат язгуур авч болно.
- Язгуурын тодорхойлогдох муж. Зөвхөн эерэг тооноос арифметикийн квадрат язгуур авч болно.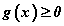 - Язгуурын утгын муж. Тэнцэтгэл бишийн хоёр талыг квадрат зэрэг дэвшүүлснээр бид сөрөг хэсгийг алга болгоно. Үүнээс үүдэн гадны шийд бий болох талтай. Энэ тэнцэтгэл биш нь тэдгээрийг хязгаарлах юм.
- Язгуурын утгын муж. Тэнцэтгэл бишийн хоёр талыг квадрат зэрэг дэвшүүлснээр бид сөрөг хэсгийг алга болгоно. Үүнээс үүдэн гадны шийд бий болох талтай. Энэ тэнцэтгэл биш нь тэдгээрийг хязгаарлах юм.
Сурагчид эхний 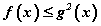 тэнцэтгэл бишийг л нухаад нөгөө хоёрыг таг мартдагт л гол алдаа оршдог. Үр дүн нь буруу бодолт, оноо алдах явдал. Иррационал тэнцэтгэл биш нилээд төвөгтэй сэдэв учраас доорх жишээнүдийг сайн ойлгон авахыг хичээгээрэй.
тэнцэтгэл бишийг л нухаад нөгөө хоёрыг таг мартдагт л гол алдаа оршдог. Үр дүн нь буруу бодолт, оноо алдах явдал. Иррационал тэнцэтгэл биш нилээд төвөгтэй сэдэв учраас доорх жишээнүдийг сайн ойлгон авахыг хичээгээрэй.
Бодлого 5.041 Москвагийн Улсын их сургууль ЭШ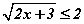 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.
Бодлого 5.042 Москвагийн Улсын их сургууль ЭШ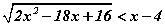 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.
Бодлого 5.043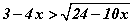 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.
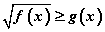 хэлбэрийн тэнцэтгэл биш
хэлбэрийн тэнцэтгэл биш
Дээрх тэнцэтгэл бишийн тодорхойлогдох муж нь f (x) ≥ 0. Энэхүү тодорхойлогдох мужийн ямар нэгэн x -ийн утганд g (x) < 0 байлаа гэе. x -ийн тухайн утганд тэнцэтгэл бишийн зүүн хэсэг тодорхойлогдон сөрөг биш утгатай байхад баруун хэсэг g (x) < 0 болж байгаа тул x -ийн эдгээр утгууд тэнцэл бишийн шийд болох нь илэрхий.
Тодорхойлогдох мужийн бусад утгуудад g (x) ≥ 0 тул тэнцэтгэл бишийн хоёр тал хоёулаа сөрөг биш болох учраас тэдгээрийг квадрат зэрэг дэвшүүлж болно. Иймээс 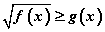 тэнцэтгэл биш нь
тэнцэтгэл биш нь 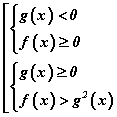 гэсэн эн чацуу тэнцэтгэл бишийн системд шилжинэ. Сүүлийн системд f (x) ≥ 0 шаардлага ороогүйг тэмдэглэе. Учир нь f(x)>g2(x)≥ 0 биелэгдэж байгаа тул f (x) ≥ 0 шаардлага хэрэггүй.
гэсэн эн чацуу тэнцэтгэл бишийн системд шилжинэ. Сүүлийн системд f (x) ≥ 0 шаардлага ороогүйг тэмдэглэе. Учир нь f(x)>g2(x)≥ 0 биелэгдэж байгаа тул f (x) ≥ 0 шаардлага хэрэггүй.
Эндээс харахад ийм тэнцэтгэл бишийг бодоход хоёр систем үүсэх бөгөөд сүүлийн шийдийг гаргахдаа системийн шийдүүдийг давхцал бус нэгтгэлийг авах ёстой. Үүнийг сайн анхаарах хэрэгтэй. Жишээ авч үзье.
Бодлого 5.044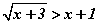 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.
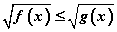 хэлбэрийн тэнцэтгэл биш
хэлбэрийн тэнцэтгэл биш
Тэнцэтгэл бишийн тодорхойлогдох муж бол 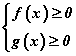 Тодорхойлогдох мужид тэнцэтгэл бишийн хоёр тал хоёулаа сөрөг биш тул квадрат зэрэг дэвшүүлж болно. Ингэснээр
Тодорхойлогдох мужид тэнцэтгэл бишийн хоёр тал хоёулаа сөрөг биш тул квадрат зэрэг дэвшүүлж болно. Ингэснээр  гэсэн эн чацуу системд шилжинэ. Энд g(x)≥f(x)≥0 гэдгээс g(x)≥0 тул тэнцэтгэл бишийг системд оруулах шаардлагагүй.
гэсэн эн чацуу системд шилжинэ. Энд g(x)≥f(x)≥0 гэдгээс g(x)≥0 тул тэнцэтгэл бишийг системд оруулах шаардлагагүй.
Эндээс хэрэгтэй мөрдлөг гарч ирнэ.
Тэнцэтгэл бишийн тодорхойлогдох мужийг олсон гэж үзвэл бид шийдийг зөвхөн тодорхойлогдох мужаас л сонгоно. Тодорхойлогдох мужаас гадна шийл байхгүй гэдэг нь ойлгомжтой. Тэгвэл анхдагч тэнцэтгэл биш нь 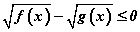 тэй эн чацуу байна. Харин тэнцэтгэл биштэй эн чацуу дээрх системийг тодорхойлогдох мужийн x -ийн хувьд
тэй эн чацуу байна. Харин тэнцэтгэл биштэй эн чацуу дээрх системийг тодорхойлогдох мужийн x -ийн хувьд 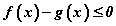 хэлбэрээр илэрхийлж болно. Эндээс тодорхойлогдох мужид
хэлбэрээр илэрхийлж болно. Эндээс тодорхойлогдох мужид 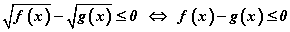 байх болно. Тэнцэтгэл бишийн тэмдэг ≥ байх тохиолдолд ч энэхүү гаргалгааг хэрэглэж болох нь ойлгомжтой. Тэгвэл
байх болно. Тэнцэтгэл бишийн тэмдэг ≥ байх тохиолдолд ч энэхүү гаргалгааг хэрэглэж болох нь ойлгомжтой. Тэгвэл 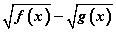 ялгаварын тэмдэг
ялгаварын тэмдэг 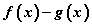 ялгаварын тэмдэгтэй ижил байна гэсэн чухал дүгнэлтэнд хүрнэ. Эндээс
ялгаварын тэмдэгтэй ижил байна гэсэн чухал дүгнэлтэнд хүрнэ. Эндээс 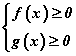 тодорхойлогдох мужид
тодорхойлогдох мужид 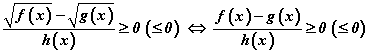 байна гэсэн бас нэгэн ашигтай мөрдлөг гарч ирнэ.
байна гэсэн бас нэгэн ашигтай мөрдлөг гарч ирнэ.
Бодлого 5.045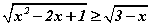 тэнцэтгэл бишийг бод.
тэнцэтгэл бишийг бод.





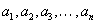 гэсэн n ширхэг ялгаатай элементийг авъя. Зөвхөн байрыг нь солих замаар бүх боломжит хувилбарыг гаргая. Ингэхдээ хувилбар болгонд n ширхэг элемент байна. Ийм байдлаар гаргаж авсан хувилбар бүрийг
гэсэн n ширхэг ялгаатай элементийг авъя. Зөвхөн байрыг нь солих замаар бүх боломжит хувилбарыг гаргая. Ингэхдээ хувилбар болгонд n ширхэг элемент байна. Ийм байдлаар гаргаж авсан хувилбар бүрийг 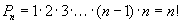
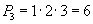 болно. Үнэхээр дээрх 3 элементээс abc, acb, bac, bca, cab, cba гэсэн 6 сэлгэмэл гаргаж болно.
болно. Үнэхээр дээрх 3 элементээс abc, acb, bac, bca, cab, cba гэсэн 6 сэлгэмэл гаргаж болно.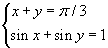 тэгшитгэлийн системийг бод.
тэгшитгэлийн системийг бод. n төрлийн обьект байлаа гэж үзье. Зургийг хар. Энд обьектудыг төлөөлүүлэн ердөө 3 төрлийн дүрсээр жишээ авъя. Эдгээр дүрсүүд дээр сэлгэмэл, гүйлгэмэл, хэсэглэл гэсэн ухагдхууныг авч үзнэ. Нийт обьектын тоо энд нэг их чухал биш гол утга учир ялгааг ойлгох нь чухал. Ухагдхууны ялгааг сайн ойлгоогүйгээс болоод ихэнх сурагчид ийм төрлийн бодлогыг бодохдоо хүндрэлтэй тулдаг.
n төрлийн обьект байлаа гэж үзье. Зургийг хар. Энд обьектудыг төлөөлүүлэн ердөө 3 төрлийн дүрсээр жишээ авъя. Эдгээр дүрсүүд дээр сэлгэмэл, гүйлгэмэл, хэсэглэл гэсэн ухагдхууныг авч үзнэ. Нийт обьектын тоо энд нэг их чухал биш гол утга учир ялгааг ойлгох нь чухал. Ухагдхууны ялгааг сайн ойлгоогүйгээс болоод ихэнх сурагчид ийм төрлийн бодлогыг бодохдоо хүндрэлтэй тулдаг. илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.