Абсалют хэмжээ /модул/
Модул гэдгийг сөрөг тооны хувьд « – » тэмдгийг « + » тэмдгээр солиход гарах эерэг тоо харин эерэг тоо болон тэгийн хувьд энэ тоо өрөө байна гэж ойлгоно. Тооны абсалют хэмжээ /модул/-ийг тэмдэглэхдээ тухайн тоог хоёр босоо зураасын дунд бичдэг.
Жишээ.
| -5 | = 5, | 7 | = 7, | 0 | = 0 г.м
Нэмэх
Ижил тэмдэгтэй хоёр тоог нэмэхдээ тэдгээрийн абсалют хэмжээг нэмээд гарсан нийлбэрт ерөнхий тэмдгийн нь тавина.
Жишээ.
( + 6 ) + ( + 5 ) = 11; ( - 6 ) + ( - 5 ) = - 11.
Өөр тэмдэгтэй хоёр тоог нэмэхдээ абсалют хэмжээ нь их тооноос абсалют хэмжээ нь бага тоог хасаад гарсан үр дүн нь абсалют хэмжээ нь их тооныхоо тэмдгийг авна.
Жишээ.
( - 6 ) + ( + 9 ) = 3; ( - 6 ) + ( + 3 ) = - 3.
Хасах
Хасах үйлдлийг хасагдагчийн тэмдгийг єєрчлєхгүй, хасагчийн тэмдгийг эсрэгээр өөрчлөөд нэмэх үйлдлээр солиж болно.
Жишээ.
( + 8 ) – ( + 5 ) = ( + 8 ) + ( – 5 ) = 3.
( + 8 ) – ( – 5 ) = ( + 8 ) + ( + 5 ) = 13.
( – 8 ) – ( – 5 ) = ( – 8 ) + ( + 5 ) = – 3.
( – 8 ) – ( + 5 ) = ( – 8 ) + ( – 5 ) = – 13.
Үржих
Хоёр тоог үржихдээ тэдгээрийн абсалют хэмжээг үржүүлнэ. Ингэхдээ үржвэр нь үржигдхүүнүүдийн тэмдэг нь ижил байвал « + » харин үржигдхүүнүүдийн тэмдэг нь єєр байвал « - » тэмдэгтэй байна. Үржвэрийн тэмдгийн дүрэм
+ · + = +
+ · – = –
– · + = –
– · – = +
Хоёр болон түүнээс олон тооны үржвэрийн тэмдгийг дараах байдлаар тодорхойлно. Сөрөг тэмдэгтэй үржигдхүүнүүдийн тоо нь тэгш байвал « + » сондгой байвал « - » тэмдэгтэй байна.
Жишээ.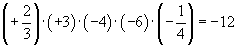
Хуваах
Хоёр тоог хооронд хуваахдаа хуваагдагчийн абсалют хэмжээг хуваагчийн абсалют хэмжээнд хувааж ногдвор нь хуваагдагч, хуваагч хоёр ижил тэмдэгтэй байвал « + », өөр тэмдэгтэй байвал « - » тэмдэгтэй байна. Энд үржвэрийн тэмдгийн дүрэм адилхан үйлчилнэ.
+ · + = +
+ · – = –
– · + = –
– · – = +
Жишээ.
( - 12 ) : ( + 4 ) = - 3; ( - 6 ) : ( - 2 ) = + 3.





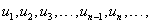 тэмдэглэгээ
тэмдэглэгээ 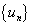
 илэрхийллийг хялбарчил.
илэрхийллийг хялбарчил.
 задаргааны 6-р гишүүнийг ол.
задаргааны 6-р гишүүнийг ол.