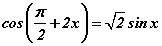 тэгшитгэлийн
тэгшитгэлийн 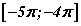 завсар дахь шийдүүдийн нийлбэрийг ол.
завсар дахь шийдүүдийн нийлбэрийг ол.
Бодолт
Хувиргалтын томьёогоор 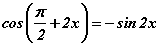 байдаг. Хувиргалтын томьёо маш олон учраас тэдгээрийг цээжлэн ашиглахад хүндрэлтэй тул өнцгийн нийлбэр, ялгаварын цөөн томьёог цээжлэн ашиглаж сурах илүү.
байдаг. Хувиргалтын томьёо маш олон учраас тэдгээрийг цээжлэн ашиглахад хүндрэлтэй тул өнцгийн нийлбэр, ялгаварын цөөн томьёог цээжлэн ашиглаж сурах илүү. 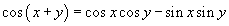 томьёогоор
томьёогоор 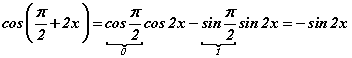 гэдгийг гарган ирэх нь алдаагүй болоод ойлгомжтой. Эндээс тэгшитгэл
гэдгийг гарган ирэх нь алдаагүй болоод ойлгомжтой. Эндээс тэгшитгэл  хэлбэрт шилжинэ. Одоо синус давхар өнцгийн
хэлбэрт шилжинэ. Одоо синус давхар өнцгийн 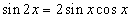 томьёог ашиглан хувиргавал
томьёог ашиглан хувиргавал
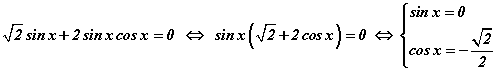 гэсэн тригнометрийн энгийн тэгшитгэлийн систем гарч ирэх ба түүнээс шийдийг олбол
гэсэн тригнометрийн энгийн тэгшитгэлийн систем гарч ирэх ба түүнээс шийдийг олбол 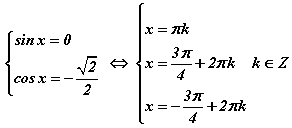 олонлог гарна. Тригнометрийн энгийн тэгшитгэлүүдийн шийдийг шууд мэддэг байхгүй бол бодлого бодох боломжгүй гэдгийг анхааруулъя. Өөрөөр хэлбэл цээжлэх хэрэгтэй.
олонлог гарна. Тригнометрийн энгийн тэгшитгэлүүдийн шийдийг шууд мэддэг байхгүй бол бодлого бодох боломжгүй гэдгийг анхааруулъя. Өөрөөр хэлбэл цээжлэх хэрэгтэй.
Одоо тэгшитгэлийн 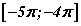 завсар дахь шийдүүдийг олох хэрэгтэй. Энд Тригнометрийн нэгж тойрог -ийг сайн ойлгосон байх ёстой. Өгөгдсөн завсар π урттай тул завсарт 1-р шийдээс 2-оос илүүгүй харин 2 ба 3 -р шийдээс нэгээс илүүгүй шийдүүд оршино. 1-р шийдийн k -д -4; -5 -ыг тавивал -4π; -5π шийдүүдэд гарна. Эдгээр нь
завсар дахь шийдүүдийг олох хэрэгтэй. Энд Тригнометрийн нэгж тойрог -ийг сайн ойлгосон байх ёстой. Өгөгдсөн завсар π урттай тул завсарт 1-р шийдээс 2-оос илүүгүй харин 2 ба 3 -р шийдээс нэгээс илүүгүй шийдүүд оршино. 1-р шийдийн k -д -4; -5 -ыг тавивал -4π; -5π шийдүүдэд гарна. Эдгээр нь 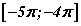 завсарт багтана. Харин 2 ба 3 -р шийдүүд 2πk үетэй тул k -гийн оронд -2; -3 тавин
завсарт багтана. Харин 2 ба 3 -р шийдүүд 2πk үетэй тул k -гийн оронд -2; -3 тавин 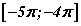 завсарт шийд байгааг шалгах хэрэгтэй. 2 -р шийдийн хувьд
завсарт шийд байгааг шалгах хэрэгтэй. 2 -р шийдийн хувьд
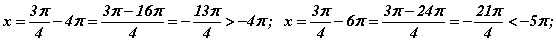 гэж гарах тул өгөгдсөн завсарт энэ бүлгээс шийд байхгүй. Харин 3 -р шийдийн хувьд
гэж гарах тул өгөгдсөн завсарт энэ бүлгээс шийд байхгүй. Харин 3 -р шийдийн хувьд
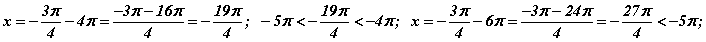 тулл -19π/4 шийд
тулл -19π/4 шийд 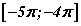 завсарт оршино. Ингээд тэгшитгэлийн
завсарт оршино. Ингээд тэгшитгэлийн 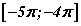 завсар дахь шийдүүдийн нийлбэр
завсар дахь шийдүүдийн нийлбэр 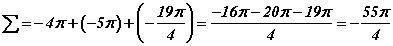 гэж гарна.
гэж гарна.
Хариу
-55π/4





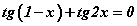 тэгшитгэлийг бод.
тэгшитгэлийг бод.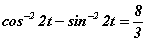 тэгшитгэлийг бод.
тэгшитгэлийг бод.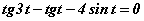 тэгшитгэлийн шийдүүд
тэгшитгэлийн шийдүүд  бол a, b, c -г ол.
бол a, b, c -г ол.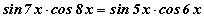 тэгшитгэлийг бодоорой.
тэгшитгэлийг бодоорой.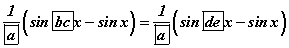 буюу
буюу 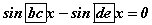 болно. Энэ ялгаварыг үржвэрт шилжүүлбэл
болно. Энэ ялгаварыг үржвэрт шилжүүлбэл 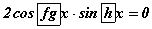 болох тул
болох тул 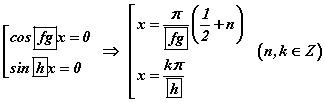 шийдтэй.
шийдтэй.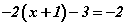 тэгшитгэлийг бод
тэгшитгэлийг бод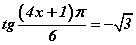 тэгшитгэлийн хамгийн бага эерэг шийдийг ол.
тэгшитгэлийн хамгийн бага эерэг шийдийг ол.