Бүх ирмэг нь 1 нэгж урттай зөв гурвалжин призмийн B, C оройнууд ба A1C1 ирмэгийн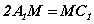 
байх M цэгийг дайрсан огтлолын талбай 
кв.нэгж , огтлогч хавтгай ABC талстай үүсгэх өнцөг 
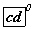, призмээс таслагдсан огтлогдсон пирамидын эзэлхүүн 
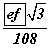куб нэгж байна.
Бодолт
Огторгуйн геометрийн ийм төрлийн бодлогууд сурагчдад асуудал үүсгэдэг. Учир нь гурван хэмжээс биетийн дүрслэлийг сайн ойлгоогүй, төсөөлөн сэтгэлтийг хөгжүүлээгүйтэй холбоотой байдаг болов уу. Бодлогын нөхцөлд өгөгдсөн зөв гурвалжин призм, призмийн огтлол, огтлогч хавтгай, талс, огтлогдсон пирамид гэх мэт ухагдхуунуудыг ойлгохгүй эсхүл мэдэхгүй бол бодлогыг бодох гэснээс шууд таах гээд оролдохоос өөр аргагүй. Үүнтэй ижил ЭЕШ 2009 A-2.4 бодлогыг бодолтыг харахын өмнө өөрөө сайн оролдоорой. Ингэхдээ
- Бодлогын нөхцөлд өгөгдсөн ухагдхуунуудыг судлан тогтоох
- Бодлогын зургийг нөхцлийн дагуу гаргах
талд илүү анхаараарай. Хэрвээ нөхцлийг зөв ойлгон зургийг гаргаж чадвал бодлогын 50 хувийг шийдсэн гэж үзэж болно. Цаашхи бодолтууд цэвэр техникийн чанартай болоод явчихна.
Санамж. Бодлогыг бодох гэж нилээд хугацаа зарцуулж магадгүй. Эхэндээ ингэх нь зүйн хэрэг. Зарим сурагчид нэг бодлогыг ийм удаан бодвол яаж шалгалт өгөх вэ? гэж буруу ойлгодог. Ийм төрлийн хэдэн бодлогыг хүний бодсонг харах биш өөрөө шийдсний дараа зарцуулах хугацаа багасан, ямар энгийн зүйл байсныг ойлгох нь математикаас авах таашаал юм шүү. Иймээс ижил төрлийн бодлогын бодолтыг харах гэж яарах хэрэггүй.
Хариу
a=4; b=8; c=6; d=0; e=1; f=3
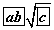байна.
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.