r=2 см радиустай тойргийн төвөөс нэг зүгт 600 ба 1200 градусийн өнцөгт тулсан паралел хоёр хөвчийг татан тэдгээрийн төгсгөлүүдийг холбоход үүсэх трапецийн талбайг ол.
Бодолт
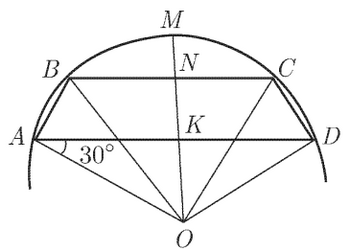Бодлогын нөхцлөөр зургийг гаргаж чадаж байх нь геометрийн бодлогыг бодох үндэс гэдгийг дахин сануулъя. Зургийг гаргахад та тойргийн хөвч, төв өнцөг ойлголтуудыг мэдэж байх ёстой. Эдгээрийг мэдэхгүй бол Төв өнцөг, түүний шинжүүд хичээлийг үзээрэй.
Бодлогын нөхцлөөс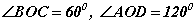 
байна. Трапецийн талбайг 
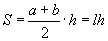томьёогоор олдог. Иймээс бид трапецийн сууриуд болох BC, AD хэрчмүүдийн уртыг олох хэрэгтэй. OB=OC=r, BOC өнцөг 60 градус гэдгээс BOC нь адил талт гурвалжин тул BC=r байна. Тэгвэл хөвчүүдэд перпендикуляр OM радиусийг татвал 
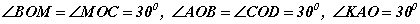гэдэг нь тодорхой болно. Хөвч хоёр радиусаар үүсэхийн дээр OM радиус хөвчүүдэд перпендикуляр учраас AD=2AK байна. Харин AKD тэгш өнцөгт гурвалжингаас косинусийн тодорхойлолтоор AK=AO·cos300 байна. Эндээс 
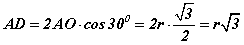гэж гарснаар трапецийн сууриуд болох BC, AD хэрчмүүдийн уртыг олсон. Одоо трапецийн өндөр NK -г олох хэрэгтэй.
Санамж: Зурагт OM радиус хөвчүүдэд яг перпендикуляр байдлаар харагдахааргүй зурагдсан байгаа. Бодлогын зургийг яг гаргана гэдэг хэцүү бөгөөд хугацаа их зарцуулах тул баримжаа зураг гаргаад бусдыг санаандаа буулгаад явж сурахыг зөвлөе.
Трапецийн өндөр NK=NO-OK -гэдэг нь зургаас тодорхой. OK нь AKD тэгш өнцөгт гурвалжны 30 градусийн эсрэг орших тал тул синусийн тодорхойлолтоор OK=r/2 гэдэг нь тодорхой. Харин NO нь BOC адил талт гурвалжны өндөр тул BNO тэгш өнцөгт гурвалжинд Пифагорийн теоремийг бичвэл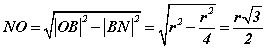 
гэж гарна. Эндээс трапецийн өндөр 
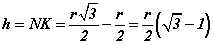байна. Шаардлагатай өгөгдлүүдийг олсон тул трапецийн талбай 
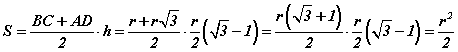байх ба нөхцлөөр r=2 см радиустай тойрог гэсэн тул талбай 2 см2 гэж гарна.
Хариу
2
функцийн графикийн (0,-1) цэгт татсан шүргэгч шулуун ба координатын тэнхлэгүүдээр хашигдсан мужийн талбайг ол.
тэнцэтгэл бишийн хамгийн их бүхэл шийдийг ол.