A(2,1); B(3,0); C(1,5) оройнуудтай гурвалжин мохоо өнцөгт гурвалжин гэдгийг батлан мохоо өнцгийн косинусийг ол.
Бодолт
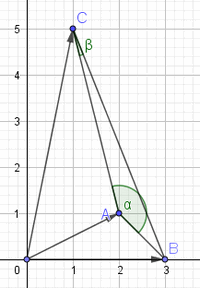 Өгөгдсөн цэгүүдийг координатийн хавтгайд байгуулаад гурвалжинг үүсгэвэл гурвалжин мохоо өнцөгт гэдэг нь шууд харагдана. Гэхдээ мохоо өнцгийн косинусийг зургаар тодорхойлох боломж муу. Бодолтыг илүү ойлгомжтой болгох үүднээс зураг орууллаа. AB ба AC, BA ба BC векторуудийн хоорондох өнцгийг α, β гэж үзье. Эхлээд AB ба AC хоорондох өнцөг α -г авч үзье. Гурвалжны дүрмээр
Өгөгдсөн цэгүүдийг координатийн хавтгайд байгуулаад гурвалжинг үүсгэвэл гурвалжин мохоо өнцөгт гэдэг нь шууд харагдана. Гэхдээ мохоо өнцгийн косинусийг зургаар тодорхойлох боломж муу. Бодолтыг илүү ойлгомжтой болгох үүднээс зураг орууллаа. AB ба AC, BA ба BC векторуудийн хоорондох өнцгийг α, β гэж үзье. Эхлээд AB ба AC хоорондох өнцөг α -г авч үзье. Гурвалжны дүрмээр 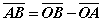 байна гэдгээс
байна гэдгээс 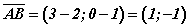 координаттай. Үүний адилаар
координаттай. Үүний адилаар 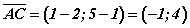 координаттай. Вектор хоорондын өнцгийн косинусийг тооцох
координаттай. Вектор хоорондын өнцгийн косинусийг тооцох 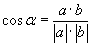 томьёог ашиглахын тулд AB ба AC векторуудийн урт, скялар үржвэрийг олох хэрэгтэй. AB ба AC векторуудийн координатуудыг мэдэж байгаа учраас векторийн уртыг олох
томьёог ашиглахын тулд AB ба AC векторуудийн урт, скялар үржвэрийг олох хэрэгтэй. AB ба AC векторуудийн координатуудыг мэдэж байгаа учраас векторийн уртыг олох 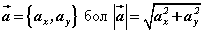 томьёогоор
томьёогоор 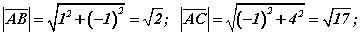 гарна. Хавтгай дахь векторуудийн скялар үржвэрийн
гарна. Хавтгай дахь векторуудийн скялар үржвэрийн 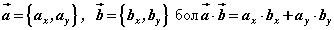 томьёогоор
томьёогоор 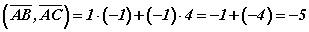 тэнцүү. Эндээс
тэнцүү. Эндээс 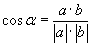 томьёогоор
томьёогоор 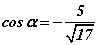 гэж гарах бөгөөд косинусийн утга тэгээс бага байгаа нь α өнцөг мохоо гэдгийг батлах тул β өнцгийг тооцох шаардлагагүй болно.
гэж гарах бөгөөд косинусийн утга тэгээс бага байгаа нь α өнцөг мохоо гэдгийг батлах тул β өнцгийг тооцох шаардлагагүй болно.
Жич: Бодолтыг ойлгохгүй бол Векторийн үйлдлүүд хичээлийг үзээд дахин хараарай.
Хариу
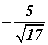





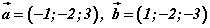 бол
бол 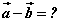
 тэгшитгэлийг бод.
тэгшитгэлийг бод.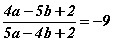 бол
бол 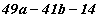 илэрхийллийн утгыг ол.
илэрхийллийн утгыг ол.